Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 62
No cálculo de uma integral dupla sobre uma região , obtivemos uma soma de integrais iteradas como a que segue:
Esboce a região e expresse a integral dupla como uma integral iterada com ordem de integração contrária.
Passo 1
Fala, gente bonita! Tudo show?
A questão nos deu uma soma de integrais e pede pra gente esboçar a região (ou seja, analisando os limites de integração) e expressar uma nova integral se a gente mudar a ordem de integração: em vez de ser , seria Massa?
Passo 2
Para esboçar a região de integração, vamos olhar primeiro para a primeira integral. As informações que temos sobre os limites de integração são esses aqui, ó:
(É como está expressa no gráfico abaixo como reta vermelha, blz?)
Já na segunda integral, temos
(Expressa pela reta azul no gráfico abaixo).
Assim, o domínio de integração é:
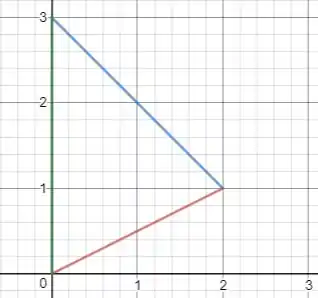
Observe que estamos trabalhando com uma região de tipo II, ou seja, os pontos no eixo são bem definidos, enquanto no eixo estamos trabalhando com funções.
Passo 3
Agora vamos inverter a ordem de integração, como a questão pede.
Para a primeira integral, teremos:
Já para a segunda integral, temos
Assim, teremos:
Observe que temos, para , limites de integração iguais nas duas integrais, e que para a primeira integral vai de
E na segunda integral
Então poderemos resumir a nova expressão da integral na região como essa aqui, ó:
Show! 😊