Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 12a
Desenhe um exemplo de uma região que seja
- Tanto do tipo I quanto do tipo II;
- Nem do tipo I nem do tipo II.
Passo 1
Faaaaaala minha turminha, tudo na paz?
Bom, no item (a) o problema pede para desenharmos uma região que é do tipo I e II.
Vamos utilizar softwares para plotar as regiões. Mas antes disto, o que é região do tipo I e uma do tipo II?
Uma região do tipo I é uma região limitada acima e abaixo por uma curva, além disto, é limitada lateralmente por retas verticais. Portanto, o seu domínio é:
Escrevemos a integral do tipo I da seguinte forma:
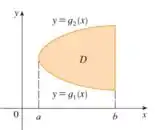
Já uma região do tipo II é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Portanto, temos o seguinte domínio:
A integral do tipo 2, é escrita como:
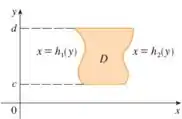
Podemos escolher qualquer função para fazer esta representação, desde que respeite os critérios mencionados acima.
Bora lá começar!
Passo 2
Vamos começar pelo item (a), esboçando regiões do tipo I e II.
Lembra, que podemos escolher qualquer função para representar, desde que obedeça aos critérios que mencionamos no passo 1.
O gráfico do tipo I, tem que ter essa cara:
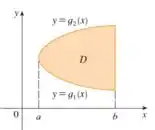
Podemos escolher as seguintes funções para esboçar a região:
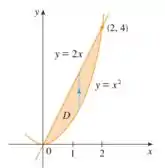
Escolhemos aleatoriamente, mas repara como ela segue às regras para o tipo I. Temos em relação ao eixo a variação entre uma função mais abaixo e uma função mais acima, já no eixo x varia de até .
Passo 3
Agora vamos fazer uma região do tipo II.
Também podemos escolher qualquer função, desde que respeite as regras para o tipo II. Que é:
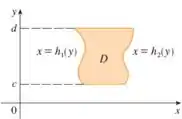
Podemos esboçar a seguinte região:
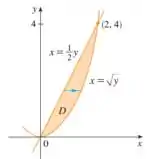
Também escolhemos duas curvas quaisquer, mas que respeitam os critérios para uma região do tipo II. Observe que em relação ao eixo , varia de uma função a esquerda até uma função a direita e no eixo de até .
Você reparou que as figuras são iguais e muda apenas a função?
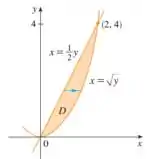
Esse tipo de região é tipo I e tipo II. Isso acontece porque conseguimos isolar e , e escrever um em função do outro.
Resposta
Tipo I: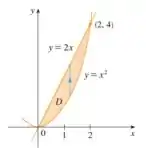 
Tipo II: 