Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 65
Use a geometria ou simetria, ou ambas, para calcular a integral dupla
é o retângulo ,
Passo 1
Faala, pessoal!
Nessa questão a gente precisa calcular uma integral dupla, mas não vamos calcular normalmente!
A questão pediu pra usarmos geometria ou simetria, ou ambas.
Geometria nós vamos usar pra comparar a integral com o volume de um sólido, e ai calculando o volume, nos já temos o valor da integral!
Spoiler: antes de fazer isso, a gente pode separa essa integral em uma soma de duas integrais...
Já simetria está relacionado com funç��es pares ou ímpares.
Uma função par é aquela que:
E então:
Já uma função ímpar é quando:
E:
Percebe que simetria é usada principalmente em intervalos do tipo , mas os intervalos do nosso domínio são do tipo .
Então pra resolver essa questão, a gente vai usar geometria!
Primeiro vamos separar integral em uma soma de integrais, ver quais são os sólidos que cada uma delas representa, e calcular os volumes desses sólidos. No final, a integral vai ser a soma dos dois volumes.
Passo 2
A nossa integral é:
Nós vamos identificar cada uma dessas integrais como o volume de um sólido, então vamos dar nomes a isso:
Calculando cada um dos volumes, vamos ter:
Passo 3
Vamos para o primeiro volume:
Essa integral representa o volume embaixo do gráfico de , sobre o domínio , que é esse:
A superfície é um plano. A gente consegue esboçar ela desenhando a reta no plano e depois estendendo para o 3D:
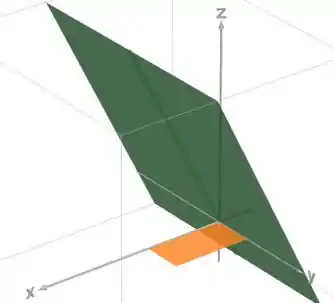
Como estamos só no domínio , o sólido fica assim:
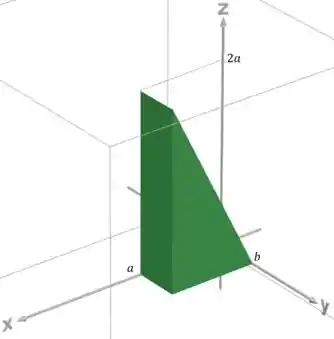
Esse sólido é metade de um paralelepípedo, de arestas , e .
Como o volume de um paralelepípedo é o produto das arestas, nosso volume fica assim:
Passo 4
Agora calculando o segundo volume:
Percebe que vai ser bem parecido com o primeiro?
O domínio é o mesmo:
E o sólido é a região embaixo do gráfico do plano sobre esse domínio:
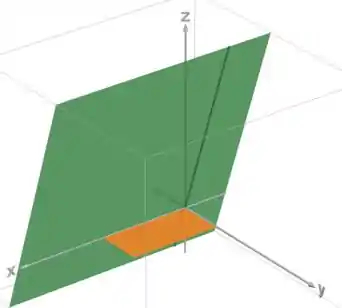
O sólido fica assim:
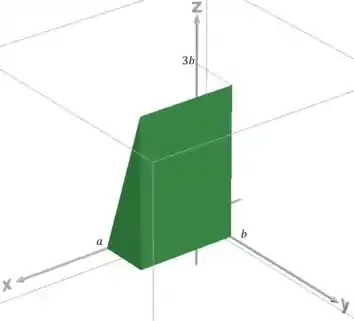
Que é metade de um paralelepípedo de arestas , e . Então o volume fica:
Passo 5
A integral vai ser a soma dos dois volumes: