Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 2
Considere a transformação φ de ℝ2 em ℝ2 dada por x = u + v e y = u − v. Desenhe φ (B)
- sendo B a reta v = 0.
- sendo B o quadrado 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
Passo 1
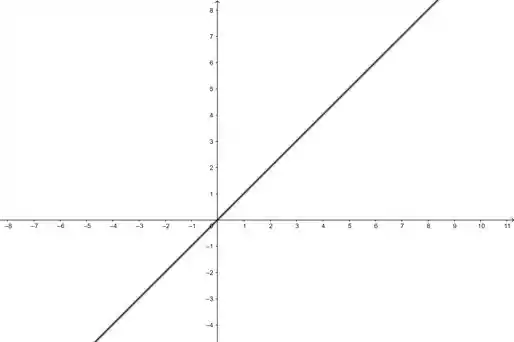
- Quando usamos a reta , temos nossa transformação dada como:
- Bom, a região é um quadrado de vértices .Aplicando a transformação em cada ponto, temos os novos vértices:
Ou seja, temos que podemos conhecemos bem. Fica assim o desenho então:
Passo 2
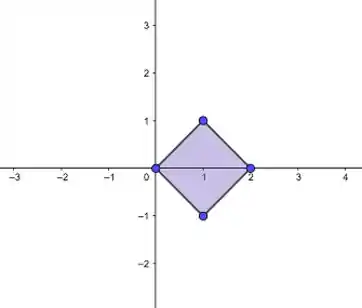
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere a aplicação definida por x = u v e y = v - u Determine a imagem D no plano x y do retângulo R no plano u v de vértices 0,1 , 1,1 , 1,2 e 0,2 .
Calcue ∫ ∫ D cos x - y x + y d x d y , onde D é a região do plano x y limitada por x + y = 1 , x = 0 e y = 0 .
Considere a aplicação g definida pelas equações x = u + v e y = v - u 2 Utilizando g , calcule ∫ ∫ D x - y + 1 4 - 1 2 d x d y , onde D é a imagem no plano x y da região Q no plano u v limitada pelas
Calcule a integral iterada. ∫ 0 1 ∫ x e x 3 x y 2d yd x
Calcule a integral iterada. ∫ 0 1 ∫ 0 x cos x 2d yd x