Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.4 - Ex. 54

Calcule a integral indefinida:

int (e^x)/(sqrt(e^(2 x) + 1)) d x

Passo 1

Primeiro vamos fazer umas substituições para tirar essa exponencial, para ficar melhor de trabalhar:

u = e^x

d u = e^x d x

Substituindo temos:

int (e^x)/(sqrt(e^(2 x) + 1)) d x = int (1)/(sqrt(u * u + 1)) d u = int (1)/(sqrt(u^2 + 1)) d u

Passo 2

Para resolver essa integral vamos fazer uma substituição trigonométrica, temos que a expressão é da forma sqrt(x^2 + a^2) , nesse formato de expressão vamos fazer u = a tg theta e utilizar a identidade trigonométrica 1 + tg^2 theta = sec^2 theta :

u = tg theta

d u = sec^2 theta d theta

Substituindo temos:

int (1)/(sqrt(u^2 + 1)) d u = int (1)/(sqrt(tg^2 theta + 1)) sec^2 theta d theta

Agora usando a identidade trigonométrica:

int (1)/(sqrt(tg^2 theta + 1)) sec^2 theta d theta = int (1)/(sqrt(sec^2 theta)) sec^2 theta d theta = int (1)/(sec theta) sec^2 theta d theta = int sec theta d theta

Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:

int sec x d x = ln |sec x + tg x| + C

Aplicando:

int sec theta d theta = ln |sec theta + tg theta| + C

Passo 3

Calma, não terminou ainda, vamos ter que voltar para a variável original x :

int (e^x)/(sqrt(e^(2 x) + 1)) d x = int (1)/(sqrt(u^2 + 1)) d u = int sec theta d theta = ln |sec theta + tg theta| + C

Temos que u = tg theta , assim vamos usar o triângulo retângulo abaixo para achar sec theta e tg theta :

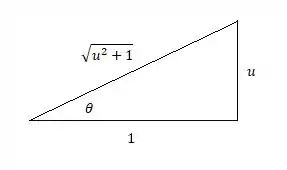
Assim os valores de sec theta e tg theta são:

sec theta = (1)/(cos theta) = (1)/((1)/(sqrt(u^2 + 1))) = sqrt(u^2 + 1)

tg theta = (u)/(1) = u

Pronto, ficamos então com:

int (e^x)/(sqrt(e^(2 x) + 1)) d x = ln |sec theta + tg theta| + C = ln |sqrt(u^2 + 1) + u| + C =

= ln |sqrt((e^x)^2 + 1) + e^x| + C = ln |sqrt(e^(2 x) + 1) + e^x| + C

Resposta

int (e^x)/(sqrt(e^(2 x) + 1)) d x = ln |sqrt(e^(2 x) + 1) + e^x| + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida: ∫ x 3 x 2 - 9d x
Calcule a integral indefinida: ∫ t 5 t 2 + 16d t
Calcule a integral indefinida: ∫ 5 x + 4 x 3 x 2 + 1d x
Calcule a integral indefinida: ∫ 1 - 4 t 2 3 2 d t
Calcule a integral indefinida: ∫ 1 + x 2 x 3d x