Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 16
- Encontre desigualdades que descrevam uma bola oca com diâmetro de cm e espessura de cm. Explique como você posicionou o sistema de coordenadas que escolheu.
- Suponha que a bola seja cortada pela metade. Escreva desigualdades que descrevam uma das metades.
Passo 1
Vamos lá galerinha, tudo bom? Vejam que precisamos encontrar algumas desigualdades, que descrevaa uma bola oca e essa mesma bola cortada pela metade.
Por falar em bola, faz muito sentido utilizarmos coordenadas esféricas. Vamos recordar o que é cada item nas coordenadas esféricas? Veja a imagem:
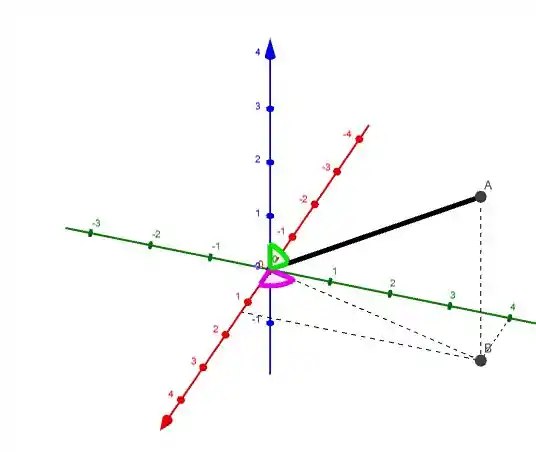
A reta em preto significa o raio, enquanto em roxo temos o ângulo e em verde o ângulo .
Temos que identificar quais valores serão obtidos para cada uma dessas coordenadas e escrever isso matematicamente.
Passo 2
- Vamos lá, temos então uma camada externa de 0,5 cm de espessura e um diâmetro de 30 cm, porque vai em todas as direções:
Veja que é o raio da esfera em que há sólido, ou seja, se a esfera é oca não há sólido em seu interior, apenas em sua espessura. Se o diâmetro é o raio externo e a esperssura é . Então:
Para ter a bola toda temos:
E por último, temos a direção da bola em :
Passo 3
Com a bola cortada na metade vamos ter a mesma desigualdade para :
Para ter a bola na metade temos:
E por último, temos a direção da bola em :