Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 13

Calcule a integral tripla.

∭ E 6 x y   d V

Onde, E está abaixo do plano z = 1 + x + y e acima do plano x y limitada pelas curvas y = x , y = 0 e x = 1

Passo 1

Show ein galerinha? Vamos calcular uma integral tripla:

∭ E 6 x y   d V

Que está abaixo do plano

z = 1 + x + y

E acima do plano x y limitada pelas curvas y = x , y = 0 e x = 1 .

Bem... vamos lá, primeiro passo é conseguir aplicar os limites de integração de forma adequada. Depois? ora depois é só calcular a integral.

Precisamos entender primeiramente qual o domínio que estamos trabalhando. A região do espaço está abaixo de um plano e acima do plano x y . Portanto, temos:

0 ≤ z ≤ 1 + x + y

Agora, precisamos entender o comportamento da região no plano x y . Ela pode ser escrita tanto do tipo I quanto do tipo II.

Uma integral do tipo I é uma integral que “varre” um gráfico de uma função até outra função no sentido vertical, ou seja, em relação à variável y . Enquanto que na direção de x utilizaremos o valor dos pontos de intersecção.Veja o exemplo:

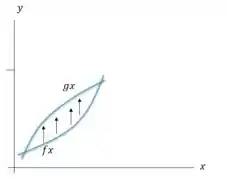
Uma integral do tipo II é exatamente ao contrário, utilizará funções de x e manterá y   como um valor fixo.

Escrevendo-a como do tipo I, temos:

0 ≤ x ≤ 1

0 ≤ y ≤ x

Portanto, temos a seguinte integral:

∫ 0 1 ∫ 0 x ∫ 0 1 + x + y 6 x y   d z d y d x

Muito cuidado na hora de colocar a ordem! O resultado final deve ser um número!

Passo 2

Precisamos começar integrando a variável z Portanto,

∫ 0 1 ∫ 0 x ∫ 0 1 + x + y 6 x y   d z d y d x = ∫ 0 1 ∫ 0 x 6 x y   z 0 1 + x + y   d y d x

∫ 0 1 ∫ 0 x 6 x y ⋅ 1 + x + y   d y d x

Fazendo a operação distributiva:

∫ 0 1 ∫ 0 x 6 x y + 6 x 2 y + 6 x y 2   d y d x

Passo 3

Agora, precisamos integrar em relação a y . Logo,

∫ 0 1 ∫ 0 x 6 x y + 6 x 2 y + 6 x y 2   d y d x

3 x y 2 + 3 x 2 y 2 + 2 x y 3 0 x =   3 x x + 3 x 2 x + 2 x x 3 / 2

Simplificando:

3 x 2 + 3 x 3 + 2 x 5 2

Então temos:

∫ 0 1 3 x 2 + 3 x 3 + 2 x 2

Passo 4

Resolvendo a integral mais “externa”:

∫ 0 1 3 x 2 + 3 x 3 + 2 x 5 2   d x = 3 x 3 3 + 3 x 4 4 + 2 x 7 2 7 2  

Por fim, basta simplificarmos:

x 3 + 3 x 4 4 + 4 7 ⋅ x 7 2 0 1

1 + 3 4 + 4 7 = 65 28

Resposta

∭ E 6 x y   d V = 65 28

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do sólido dado. Abaixo da superfície z = x 2 y e acima do triângulo no plano x y com vértices 1,0 ,2,1e4,0 .
Determine o volume do sólido dado. Uma das cunhas obtidas pelo corte do cilindro x 2 + 9 y 2 = a 2 pelos planos z = 0 e z = m x .
Uma luminária tem três lâmpadas, cada uma com vida média de 800h o r a s . Se modelarmos a probabilidade de falha das lâmpadas por uma função densidade exponencial com média 800 , determine a probabil
Utilize a transformação x = u 2 , y = v 2 , z = w 2 para determinar o volume da região limitada pela superfície x + y + z = 1 e pelos planos coordenados.
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro y = x 2 e pelos planos z = 0 e y + z = 1