Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 18
Calcule a integral tripla.
Onde é limitado pelo cilindro e pelos planos e no primeiro octante.
Passo 1
Fala aí!
Nesse exercício, precisamos calcular uma integral tripla:
Sobre essa região que ele descreve.
Nosso primeiro passo vai ser usar essa região pra definir os limites de integração das variáveis. Pra isso, a gente vai descrever como uma região do tipo , que é quando está entre duas funções de e , e pertencem a um domínio no plano .
Assim, a gente vai conseguir escrever a nossa integral como uma integral iterada, e calcular! Lembra que sempre calculamos integrais múltiplas de dentro pra fora.
Passo 2
Primeiro vamos olhar pras superfícies que delimitam nossa região:
Como estamos no primeiro octante, já sabemos que .
Vamos ver como são essas superfícies:
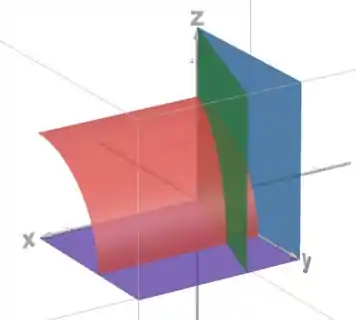
Em vermelho é o cilindro , e em azul, verde e roxo os planos e , respectivamente.
Percebe que nossa região fica entre esses planos verde e azul:
E isso já nos dá os limites de :
Descrevendo nossa região como do tipo , temos:
Então basta descobrimos quem é , que vai ser a projeção da região no plano :
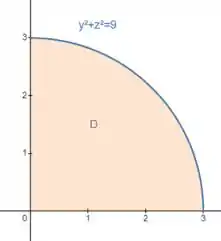
Como estamos na regi��o onde e são positivos, podemos reescrever como:
E ai definimos os limites de e como:
E os de , que já sabemos:
Percebe que como os limites de e dependem de , a integral de vai ser a última. Nossa integral iterada fica assim:
Passo 3
Começamos integrando em função de , considerando e constantes:
Calculando nos limites:
A gente pode cancelar a raiz com o quadrado e:
Colocando o pra fora da integral:
Passo 4
Agora integramos em função de , com constante:
Como é constante, pode sair dessa integral:
Então:
Resolvendo nos limites de integração:
Passo 5
Pra terminar, vamos integral em função de :
Vamos colocar pra fora, e fazer a distributiva com o :
Resolvendo a integral:
Como , fica assim:
E então:
Ou seja: