Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 9

Calcule a integral tripla.

∫ ∫ ∫ E 6 x y   d V , onde E está abaixo do plano z = 1 + x + y e acima da região do plano x y limitada pelas curvas y = x , y = 0 e x = 1 .

Passo 1

Fala, gente boa! Tudo beleza?

Esse exercício pede pra gente calcular a integral tripla:

∫ ∫ ∫ E 6 x y   d V

Onde E está abaixo do plano z = 1 + x + y e acima da região do plano x y limitada pelas curvas y = x , y = 0 e x = 1 .

Uma integral tripla em relação a V é uma integral que está buscando o volume de um sólido:

V E = ∭ E d V

Bom, então falta o que falta para calcularmos essa integral tripla são os limites de integração para cada variável, x , y e z .

Então nosso objetivo nessa questão é olharmos o sólido tridimensional e sua projeção no plano x y , que é a região E , para entendermos qual o limite de integração de cada variável.

Com os limites de integração em mãos, é só arranjarmos a integral na ordem que acharmos mais prático e calcular nossa integral iterada, começando da integral de dentro até a integral mais externa.

Bora!

Passo 2

Vamos entender qual a nossa região E de integração com a descrição que o enunciado nos deu. E está abaixo do plano

z = 1 + x + y

Como o volume que queremos é justamente o que está abaixo da superfície da função, z é a função que vamos integrar:

z = f ( x , y ) = 1 + x + y

Os limites de integração nós pegamos no plano x y . E é a região do plano x y limitada pelas curvas y = x , y = 0 e x = 1 :

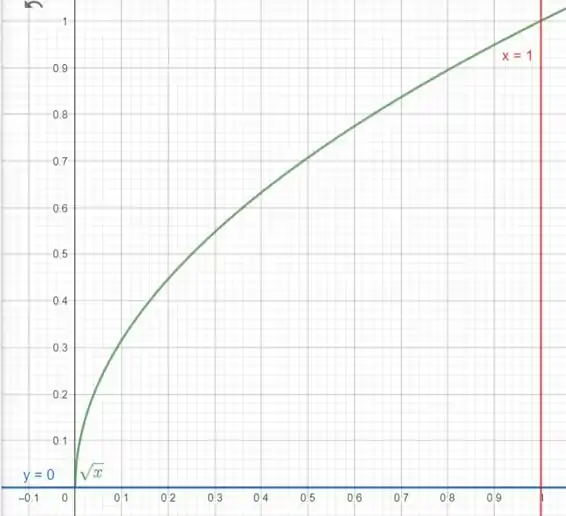
Olhando nossa imagem, vemos que:

0 ≤ x ≤ 1

0 ≤ y ≤ x

Ou seja, temos uma região do Tipo I, onde x está entre duas constantes e y entre funções.

Já nosso z , como nossa função está acima do plano x y onde z ≥ 0 (positivo) temos que:

0 ≤ z ≤ 1 + x + y

Então, a integral vai ficar assim:

∫ ∫ ∫ E 6 x y d V = ∫ 0 1 ∫ 0 x ∫ 0 1 + x + y 6 x y   d z   d y   d x

Veja que a gente coloca “por dentro” as integrais que tem variáveis nos limites de integração, para facilitar o cálculo.

Passo 3

Agora vamos efetivamente calcular a integral tripla:

∫ 0 1 ∫ 0 x ∫ 0 1 + x + y 6 x y   d z   d y   d x

Começando pela integral em função de x , mais “de dentro”. Aqui vamos tratar as demais variáveis como constante:

= ∫ 0 1 ∫ 0 x 6 x y z 0 1 + x + y d y   d x

Aplicando os limites de integração ficamos com:

= ∫ 0 1 ∫ 0 x 6 x y + 6 x 2 y + 6 x y 2   d y   d x

Agora fazemos a integral de dentro novamente, que agora será a de y , tratando as demais variáveis como constante:

= ∫ 0 1 3 x y 2 + 3 x 2 y 2 + 2 x y 3 0 x d x

Aplicando os limites de integração:

= ∫ 0 1 3 x 2 + 3 x 3 + 2 x 2 x   d x

Agora sobrou a nossa integral “de fora”:

= x 3 + 3 x 4 4 + 4 x 7 2 7 0 1

Por fim, calculando os limites de integração:

= 1 + 3 4 + 4 7 = 65 28

Então o volume abaixo do nosso plano z   e acima de plano x y   é:

V E = ∫ 0 1 ∫ 0 x ∫ 0 1 + x + y 6 x y   d z   d y   d x = 65 28

Resposta

65 28

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando a área em termos de integral de função de uma variável real e use sua calculadora para estimar a integral.A parte da su
Calcule a integral iterada. ∫ ∫ ∫ ε x 2 ⋅ e y⋅ d V , onde E é limitado pelo cilindro parabólico z = 1 - y 2 e pelos planos z = 0 , x = 1 e x = - 1 .
Calcule a integral iterada. ∫ ∫ ∫ ε x ⋅ z⋅ d V , onde E é o sólido tetraedro com vértices (0,0,0), (0,1,0), (1,1,0) e (0,1,1).
Calcule a integral iterada. ∫ ∫ ∫ ε x ⋅ y⋅ d V , onde E é o sólido tetraedro com vértices (0,0,0), (1,0,0), (0,2,0) e (0,0,3).
Calcule a integral tripla ∭ E x + 2 y d V , onde E é limitado pelo cilindro parabólico y = x 2 e pelos planos x = z , x = y e z = 0 .