Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 44
Calcule a integral trocando a ordem de integração.
44.
Passo 1
E aê, gente bonita. Tudo beleza?
A questão nos diz que precisamos calcular a integral trocando a ordem de integração. No nosso caso, em vez de calcular , precisamos calcular . Siniiistrooo...
Presta atenção que não é só isso que temos que trocar, hein? Os limites de integração também!!!
Com as informações que temos na nossa integral dupla original dada na questão, a região de integração está entre
Representamos assim:
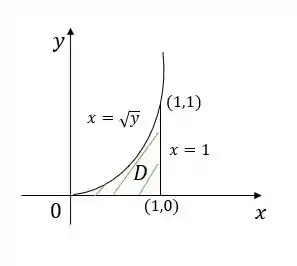
Invertendo a ordem de integração, temos que
Portanto, os limites ficarão:
Passo 2
Então, após a mudança nos limites de integração, vamos reescrever a integral
Vamos resolver de dentro pra fora, primeiro em relação a :
Substituindo, temos
Agora integrando em relação a ,
Pela técnica da substituição, seja
Então
Cancelando termos, ficaremos com
Podemos colocar nossa fração para fora da integral, como uma constante.
Pela divisão de frações, invertemos o denominador multiplicando:
Como , colocamos ele de volta:
E agora substituindo os limites de integração, teremos:
Colocando a fração em evidência,