Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.3 - Ex. 5i
Calcule.
Passo 1
Para resolver esse limite podemos pensar em apenas substituindo o valor na expressão, entretando, ao fazer isso, ficamos com a inderterminação
Devemos olhar se existe alguma forma de simplificar essa expressão, para evitar essa indeterminação, então vamo lá!
Passo 2
Vamos analisar o limite:
No numerador temos um polinômio do terceiro grau, da seguinte forma , então podemos usar a seguinte fórmula:
Assim temos e :
Passo 3
Para o denominador temos , vamos tentar achar raízes, vamos usar o valor :
Dividindo por :
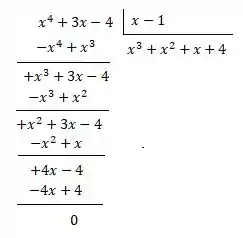
Vamos ter que:
Passo 4
Pronto, agora é só substituir no limite:
Agora é só necessário substituir o valor na expressão, e achamos a resposta!!
Resposta
Exercícios de Livros Relacionados
Ache o limite, se existir. lim x → 0 - x 2 - 5 2 x 3 - 3 x 2
Ache o limite, se existir.underset(x - 4^+)(lim) (2 x)/(16 - x^2)
Ache o limite, se existir. lim x → 9 2 x - 6 x - 9
Ache o limite, se existir. lim y → 3 y - 3 y 3 - 27
Ache o limite, se existir. lim t → 5 t - 4 t 2 - 10 t + 25