Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.1 - Ex. 1f
Calcule.
Passo 1
Vamos fazer algumas manipulações, primeiro vamos colocar em evidência no numerador e em evidência no denominador:
Podemos aqui usar a propriedade da multiplicação nesse limite:
Agora a propriedade da divisão e da subtração:
Agora vamos resolver eles separadamente.
Passo 2
No primeiro temos que:
se
Vamos ver isso graficamente com a expressão com :
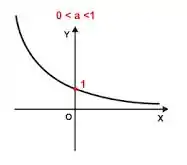
Vemos pelo gráfico que quando os valores da função tendem a zero, assim:
Passo 3
Agora no numerador:
Temos o limite de uma função constante, que a resposta é essa constante:
No outro limite vamos usar que:
se
Assim:
Passo 4
Agora no denominador:
Temos também o limite de uma função constante, que a resposta é essa constante:
E no outro limite vamos usar que:
se
Assim:
Passo 5
Por último é só juntar os resultados e pronto:
Lembre que tende a zero, pois quanto maior o valor do denominador, mais próximo de zero vai está.