Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.2 - Ex. 4b
Calcule.
Passo 1
Oi, pessoal! Para resolver esse limite, você tem que reparar que a nossa base do é fracionária. Então, para ajudar a gente a resolver os limites que tem esse tipo de base, vamos usar a informação de que:
Com
Isso se encaixa perfeitamente para o nosso caso já que nosso é igual a , e está entre e 1.
Passo 2
Uma forma de percebemos essa tendência é visualizando o gráfico da função,
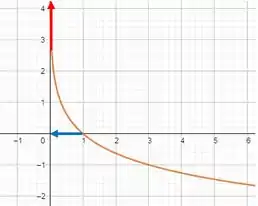
Repara que quando se aproxima de zero (como representamos pela setinha azul), a nossa função vai para infinito (como mostra a setinha vermelha).
Resposta
Exercícios de Livros Relacionados
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → 0 ( 3 - 7 x - 5 x 2 )
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → - 1 / 3 2 x + 3 1 4
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → 7 3 x + 2 2 3
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → 4 ( e x + 4 x )
Mostrar que:Se f é uma função polinomial, então lim x → a f x = f ( a ) para todo real a .Se g é uma função racional e a pertence ao domínio de g , então lim x → a g x = g ( a ) .