Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequências de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se ela for convergente, calcule a soma. Se for divergente, explique por quê.

Vamos calcular as dez primeiras somas parciais

Já deu né? Com 7 termos de já vimos que desta forma não vamos achar uma padrão, mas vamos jogar no gráfico pra ver se parece que isso vai chegar a algum limite.

Montando o gráfico temos:

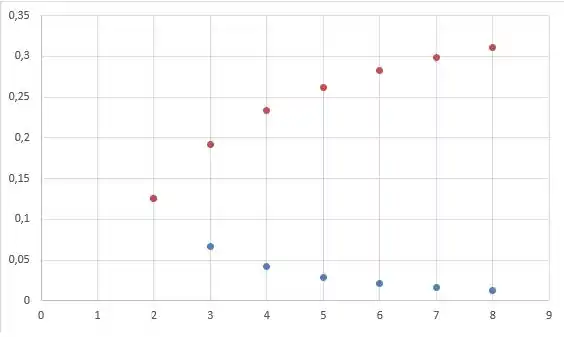
Onde os pontos azuis são os termos e em vermelho temos .

Podemos ver que os termos então se aproximando de um limite que é , o que é necessário para a convergência da série. Já os termos de parecem se aproximar de um limite, mas com poucos termos assim não podemos dizer qual seria esse limite.

Para calcular esse limite vamos ter que achar um termo geral pra soma, para isso vamos manipular um pouco o termo geral da série

Separando esse termo em duas frações

E fazendo o MMC para calcularmos os valores de e :

Portanto temos a igualdade

Distribuindo a multiplicação e em seguida colocndo em evidencia

Pela igualdade de polinômios temos o seguinte sistema

Com a segunda equação chegamos em

Substituindo na primeira

Voltando ao termo da série, temos que

Vamos agora tentar calcular alguns valores da soma?

Aqui já começamos a cancelar, presta atenção que os se cancelam, massa né?

Já cancelamos agora além do , também o , mas vamos continuar

Agora cancelamos também o . Acho que já achamos o padrão né? De maneira geral ficamos com as primeiras frações dos dois primeiros termos e com as segundas frações dos 2 ultimos termos, ou seja

Agora que temos o termo geral, vamos aplicar o limite

Fazendo o MMC

Portanto