Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 1a

Calcule ∫ C f d s , onde

a )   f x ,   y = x + y e C é a fronteira do triângulo de vértices 0 ,   0 ,   1 ,   0 e 0 ,   1 .

Passo 1

E aí, galerinha!! Vamo que vamo com o Responde Aí em mais um exercício!! :D

Para calcularmos a integral de linha, precisamos parametrizar a nossa função. Mas antes disso, precisamos notar que a nossa curva C é decomposta em três retas como mostrado a seguir:

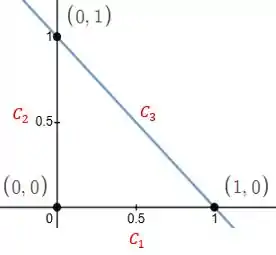
Isso nos mostra que é necessário fazer a decomposição da integral também. Logo, a nossa integral da curva total será a soma das integrais de cada reta:

∫ C f d s = ∫ C 1 f d s + ∫ C 2 f d s + ∫ C 3 f d s

Tal que essas retas podem ser escritas como:

C 1 : y = 0

C 2 : x = 0

C 3 : y = 1 - x

E parametrizadas por:

C 1 : σ t = t ,   0 ,   0 ≤ t ≤ 1 C 3 :   σ t = t ,   1 - t ,   0 ≤ t ≤ 1 C 2 : σ t = 0 ,   t ,   0 ≤ t ≤ 1

Assim, uma curva parametrizada terá sua integral dada por:

∫ C f d s = ∫ f σ t ∙ σ ' t d t

E as nossas curvas terão os valores:

C 1 : σ ' t = 1 ,   0 → σ ' t = 1 C 3 :   σ ' t = 1 ,   - 1 → σ ' t = 2 C 2 : σ ' t = 0 ,   1 → σ ' t = 1

Passo 2

Então, nossas integrais podem ser escritas como:

∫ C 1 f d s + ∫ C 2 f d s + ∫ C 3 f d s = ∫ C 1 x + y d s + ∫ C 2 x + y d s + ∫ C 3 x + y d s

Ou seja:

∫ C 1 f d s + ∫ C 2 f d s + ∫ C 3 f d s = ∫ 0 1 t + 0 1 d t + ∫ 0 1 0 + t 1 d t + ∫ 0 1 t + 1 - t 2 d t

⇒ ∫ 0 1 t d t + ∫ 0 1 t d t + ∫ 0 1 2 d t

Portanto, teremos os resultados:

∫ 0 1 t d t + ∫ 0 1 t d t + ∫ 0 1 d t = t 2 2 1 0 + t 2 2 1 0 + 2 t | 1 0

Passo 3

Agora, substituindo os intervalos de integração:

t 2 2 1 0 + t 2 2 1 0 + t | 1 0 = 1 2 1 - 0 + 1 2 1 - 0 + 2 1 - 0

Portanto:

⇒ 1 2 + 1 2 + 2 = 1 + 2

Resposta

1 + 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o trabalho realizado pela força constante f → = i → + j → para deslocar uma partícula ao longo da reta x + y = 1 , do ponto A = 0,1 aB = ( 1,0 ) .
Calcular o trabalho realizado pela força f → = 1 x + 2 , 1 y + 3 Para deslocar uma partícula em linha reta do ponto P ( 3,4 ) até Q = ( - 1,0 ) .
9. Um campo é formado por uma força f → , de módulo igual a 4 unidades de força, que tem a direção do semi-eixo positivo dos x . Encontrar o trabalho desse campo, quando um ponto material descreve no
8. Um campo de forças é dado por: f → x , y = - r → | r → | 3 Onde r → = ( x , y ) . Sob a ação desse campo, uma partícula desloca-se sob a curva x 2 + 4 y 2 = 16 no sentido horário, do ponto A ( 4 ,0
Nos exercícios 11 a 17, determinar a integral curvilínea do campo vetorial f → ao longo da curva C dada.11. f → x , y = ( x , y ) ; C é o quadrado de vértices ( - 1 , - 1 ) ,( - 1,1 ) , ( 1,1 ) e ( 1