Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 1

Calcule

int_gamma root(3)(x) d x + (d y)/(1 + y^2)

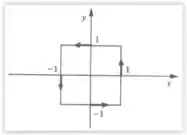
Onde gamma é a curva

Passo 1

Olhando para nossa curva, temos que perceber a necessidade de dividi-la em 4 partes. Uma vez descrita as 4 curvas e seus intervalos, só precisaremos integrá-las

Passo 2

Vamos fazer assim

A curva superior gamma_1

gamma_1 (t) = (t , 1) , 1 >= t >= - 1

A curva a esquerda gamma_2

gamma_2 (t) = (- 1 , t) , 1 >= t >= - 1

A curva inferior gamma_3

gamma_3 (t) = (t , - 1) , - 1 <= t <= 1

A curva a direita gamma_4

gamma_4 (t) = (1 , t) , - 1 <= t <= 1

Passo 3

Agora conhecendo as curvas, podemos começar a integral

Para gamma_1

x = t -> d x = d t

y = 1 -> d y = 0

Então

int_1^(- 1) root(3)(t) d t = [(3)/(4) t^((4)/(3))]_1^(- 1) = (3)/(4) - (3)/(4) = 0

Para gamma_2

x = - 1 -> d x = 0

y = t -> d y = d t

Então

int_1^(- 1) (d t)/(1 + t^2) = [arctan t]_1^(- 1) = - (pi)/(4) - (pi)/(4) = - (pi)/(2)

Para gamma_3

x = t -> d x = d t

y = - 1 -> d y = 0

Então

int_(- 1)^1 root(3)(t) d t = [(3)/(4) t^((4)/(3))]_(- 1)^1 = (3)/(4) - (3)/(4) = 0

Para gamma_4

x = 1 -> d x = 0

y = t -> d y = d t

Então

int_(- 1)^1 (d t)/(1 + t^2) = [arctan t]_(- 1)^1 = (pi)/(4) + (pi)/(4) = (pi)/(2)

Desta forma temos que

0 - (pi)/(2) + 0 + (pi)/(2) = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o valor da integral de linha, onde C é a curva dada.
Calcule o valor da integral de linha, onde C é a curva dada.
Calcule a integral de linha, onde C é a curva dada. ∫ C s e nxd x + cos ⁡ yd y C consiste na metade superior da circunferência x 2 + y 2 = 1 de ( 1 ,0 ) a ( - 1 ,0 ) e o segmento de reta de ( - 1 ,0 )
Calcule a integral de linha, onde C é a curva dada. ∫ C x 2 zd s C é o segmento de reta de ( 0 ,6 ,- 1 ) a ( 4 ,1 ,5 ) .
Calcule a integral de linha, onde C é a curva dada. ∫ C y e xd s C é o segmento de reta que liga ( 1 ,2 ) a ( 4 ,7 ) .