Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 28
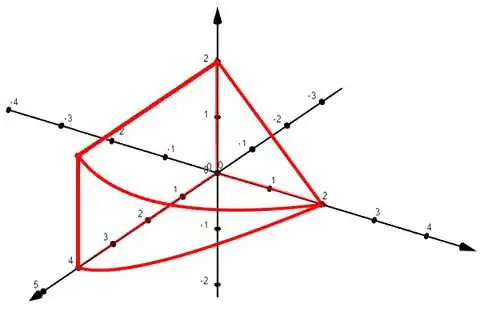
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
E aí, galera! Tudo firme?
A questão pede pra gente esboçar o sólido dado pela integral tripla:
Para entendermos onde está nosso sólido no espaço 3D e realizar o esboço, vamos pegar dos limites de integração em cada variável os limitantes do sólido.
Daí é só jogarmos em um software que traça sólidos 3D e visualizamos o sólido.
Bora lá!
Passo 2
Como temos uma integral do tipo
Então precisamos saber o que é , pelas variações temos
Repara que e são limitados em função de . Então vamos ver essas igualdades:
Para , teremos:
Como varia de até , temos que :
Essa equação representa dois planos:
e
então vamos desenhar esses planos no gráfico.
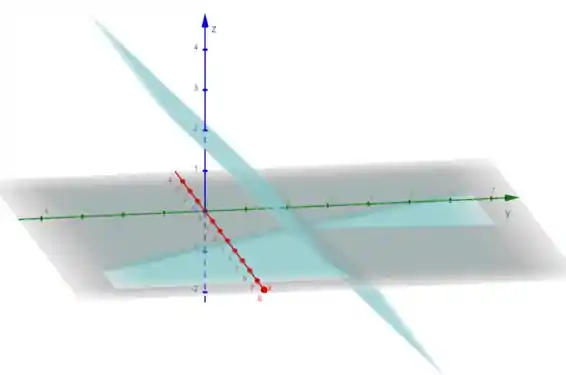
Para , teremos:
Essa equação descreve um cilindro, então vamos desenhar essa parte também no gráfico. Seguindo o mesmo raciocínio para, teremos que
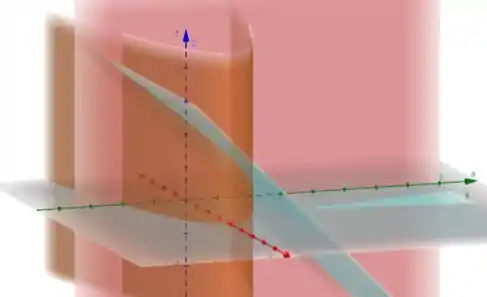
Para , temos:
Que são os planos
e
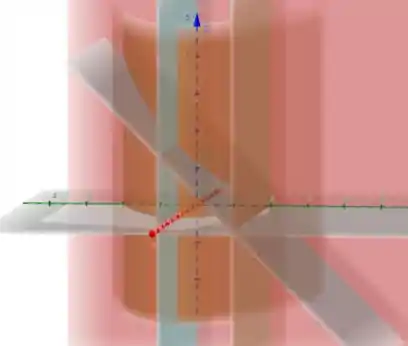
Passo 3
Ufa! Quantas superfícies, né? O sólido que nos interessa é o que está limitado por essas superfícies. Então, esboçando somente nosso sólido, ficamos com:
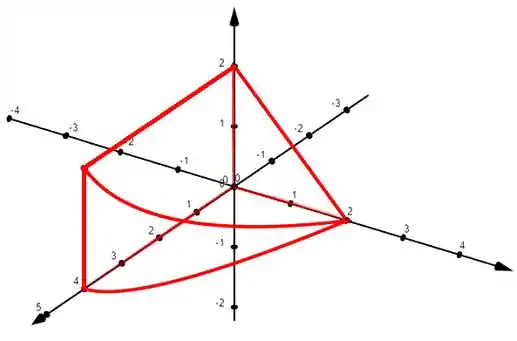
Resposta
