Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.6 - Ex. 1c

Calcule as seguintes integrais de superfície:

∬ S y 2 + z 2   d s , onde S é a superfície do sólido limitado pela parte superior da esfera x 2 + y 2 + z 2 = 1 e o cone z = x 2 + y 2 .

Passo 1

Galerinha, primeiro devemos entender a superfície S   que estamos integrando.

Sabemos que S é limitado pela parte superior da esfera x 2 + y 2 + z 2 = 1 e o cone z = x 2 + y 2 .

Vizualisando, nós temos que:

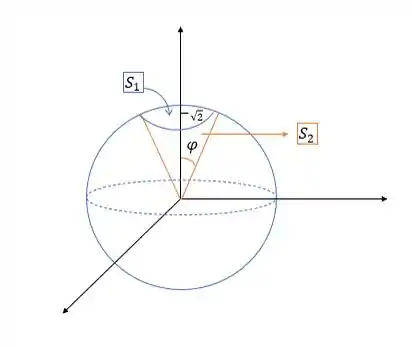
Da parte superior, temos que:

S : x 2 + y 2 + z 2 = 1

com z = x 2 + y 2 , que implica em z 2 = x 2 + y 2 .

A intersecção é:

2 z 2 = 1

que implica em: z = 2 2 .

Passo 2

Da esfera:

x 2 + y 2 + z 2 = 1

com intervalo de 0 ≤ θ ≤ 2 π 0 ≤   φ ≤ π / 4 .

Em coordanedas esféricas, temos que:

φ , θ = s e n φ cos ⁡ θ ,   s e n   φ   s e n ,   θ cos ⁡ ϕ

Logo,

| N φ , θ | = s e n   φ

Do cone:

z = x 2 + y 2

Em coordenas esféricas:

t , θ = t cos ⁡ θ ,   t   s e n   θ ,   t )

com 0 ≤ t ≤ 2 2 0 ≤ θ 2 π .

Logo,

N φ , θ = t 2 .

Passo 3

Pronto, agora podemos montar nossa integral:

∬ S y 2 + z 2 d S = ∬ S 1 y 2 + z 2 d S 1 + ∬ S 2 y 2 + z 2 d S 2

Vamos primeiro resolver ∬ S 1 y 2 + z 2 d S 1 :

∬ S 1 y 2 + z 2 d S 1 = ∬ D f φ , θ ⋅ N φ , θ   d φ d θ

⇒ ∫ 0 2 π ∫ 0 π 4 ( s e n 2   φ   s e n 2 θ + cos 2 ⁡ φ ) s e n   φ   d φ d θ = ∫ 0 2 π ∫ 0 π 4 ( se n 3 φse n 2 θ + senφ co s 2 φ ⁡   d φ d θ

Lembre-se que: s e n 3   φ = s e n   φ ( 1 - cos 2 ⁡ φ )   .

⇒ ∫ 0 2 π ∫ 0 π 4 ( s e n   φ   s e n 2 θ + sen φ  ( 1 - sen 2 θ ) ⁡   d φ d θ

Lembre-se: 1 - s e n 2 θ = cos 2 ⁡ θ .

Agora, vamos resolver a integral de dentro:

∫ 0 2 π s e n 2 θ [ - cos ⁡ φ ] 0 π 4 + cos 2 ⁡ θ   - cos 3 ⁡ φ 3 0 π 4   d θ = ∫ 0 2 π s e n 2 θ -   2 2 + 1 + cos 2 ⁡ θ - 2 2 24 + 1 3 d θ = ∫ 0 2 π 1 - cos ⁡ 2 θ 2 ⋅ 1 - 2 2 + 1 + cos ⁡ 2 θ 2 1 3 - 2 12 d θ

Passo 4

E então, vamos resolver nossa integral de fora:

∫ 0 2 π 1 - cos ⁡ 2 θ 2 ⋅ 1 - 2 2 + 1 + cos ⁡ 2 θ 2 1 3 - 2 12 d θ = 1 - 2 2 ⋅ θ 2 - s e n   2 θ 4 0 2 π + 1 3 - 2 12 ⋅ θ 2 + s e n   2 θ 4 0 2 π

Substituindo os valores do intervalo de integração:

1 - 2 2 ⋅ θ 2 - s e n   2 θ 4 0 2 π + 1 3 - 2 12 ⋅ θ 2 + s e n   2 θ 4 0 2 π = 1 - 2 2 ⋅ 2 π 2 + 1 3 - 2 12 ⋅ 2 π = π 1 - 2 2 + 1 3 - 2 12 = π 4 3 - 7 2 12 .

Passo 5

Ainda não acabamos, agora vamos resolver a integral ∬ S 2 y 2 + z 2 d S 2 :

∬ S 2 y 2 + z 2 d S 2 = ∬ D f t , θ ⋅ N ( t , θ ) d t d θ

⇒ ∫ 0 2 π ∫ 0 2 2 t 2   s e n 2 θ + t 2 ⋅ t 2   d t d θ = 2 ∫ 0 2 π ∫ 0 2 2 t 3   s e n 2 θ + t 3   d t   d θ

Primeiro resolvendo a integral de dentro:

2   ∫ 0 2 π t 4 4   s e n 2 θ + t 4 4 0 2 / 2 d θ = 2 ∫ 0 2 π 4 64   s e n 2 θ + 4 64   d θ = 2 16 ∫ 0 2 π s e n 2 θ + 1 d θ   = 2 16 ∫ 0 2 π 1 - cos ⁡ 2 θ 2 + 1   d θ

Agora, resolvendo a integral de fora:

2 16 ∫ 0 2 π 1 - cos ⁡ 2 θ 2 + 1   d θ = 2 16 θ 2 - s e n   2 θ 4 + θ 0 2 π = 2 16 ⋅ 3 ⋅ 2 π 2 = 3 π 2 16

Passo 6

Ufa, “tá” quase. Agora, retomamos a nossa equação inicial, somando os resultados.

∬ S y 2 + z 2 d S = ∬ S 1 y 2 + z 2 d S 1 + ∬ S 2 y 2 + z 2 d S 2

⇒ ∬ S y 2 + z 2 d S = π 4 3 - 7 2 12 + 3 π 2 16

⇒ ∬ S y 2 + z 2 d S = π 4 3 - 7 2 12 + 3 2 16

Resposta

π 4 3 - 7 2 12 + 3 2 16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área das seguintes superfíciesf) Superfície do paraboloide z = 5 - x 2 2 - y 2 que se encontra no interior do cilindro x 2 + 4 y 2 = 4 .
Calcule a área das seguintes superfícies: Superfície do cilindro x 2 + y 2 = 2 x limitado pelos planos z = 0 e o cone z = x 2 + y 2 .
Calcule a área das seguintes superfíciesg) Superfície da esfera de raio a centrada na origem limitada por dois planos paralelos e dois meridianos, sabendo-se que o ângulo entre os meridianos é α e a d
Considere γ o arco da parábola z = 3 - y 2 no plano y z compreendido entre as semi-retas z = z = 2 y e z = 11 2 y , com y ≥ 0 . Seja S a superfície obtida girando-se γ em torno do eixo z . Pede-se:Uma
Calcule a área das seguintes superfícies. d) Superfície da esfera x 2 + y 2 + z 2 = 12 que não está no interior do paraboloide z = x 2 + y 2 .