Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.4 - Ex. 1a

Considere γ o arco da parábola z = 3 - y 2 no plano y z compreendido entre as semi-retas z = z = 2 y e z = 11 2 y , com y ≥ 0 . Seja S a superfície obtida girando-se γ em torno do eixo z . Pede-se:

  1. Uma parametrização para S .

Passo 1

Veja a figura a seguir:

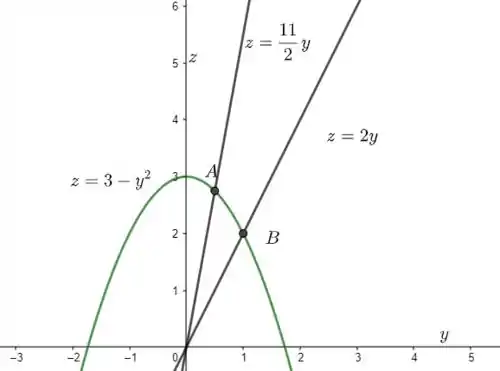
Note que estamos no plano y z ! Inicialmente, vamos determinar as coordenadas dos pontos A e B :

  1. Para o ponto A :

    2. z = 11 2 y z = 3 - y 2 ⟹ 11 2 y = 3 - y 2 ∴ 2 y 2 + 11 y - 6 = 0

    Resolvendo essa equação por Bhaskara, temos:

    y = - b ± b 2 - 4 a c 2 a y = - 11 ± 11 2 - 4 2 - 6 2 ⋅ 2 = - 11 ± 13 4

    Como vemos na figura, y > 0 . Assim,

    y = - 11 + 13 4 = 1 2

  2. Para o ponto B :

z = 2 y z = 3 - y 2 ⟹ 2 y = 3 - y 2 ∴ y 2 + 2 y - 3 = 0

Resolvendo essa equação por Bhaskara, temos:

y = - b ± b 2 - 4 a c 2 a y = - 2 ± 2 2 - 4 1 - 3 2 ⋅ 1 y = - 2 ± 4 2

Novamente, vemos que y > 0 . Assim,

y = 1

Passo 2

Como rodamos a parábola em torno do eixo z , criamos círculos no eixo x e y . Veja:

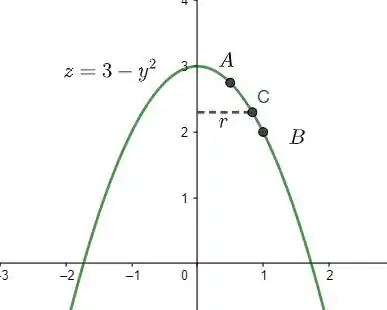
O raio desses círculos irá variar entre 1 2 ≤ r ≤ 1 . Portanto, nossa parametrização será:

φ r , θ = r cos ⁡ θ ,   r sin ⁡ θ ,   3 - r 2 ,     1 2 ≤ r ≤ 1 ,         0 ≤ θ ≤ 2 π

Veja que 0 ≤ θ ≤ 2 π para que seja possível percorrer inteiramente cada círculo!

Resposta

Uma parametrização é φ r , θ = r cos ⁡ θ ,   r sin ⁡ θ ,   3 - r 2 , com 1 2 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.) σ( u ,v )=( u ,v ,1-u-v ) ,u≥0 ,v≥0eu+v≤1 . σ( u ,v )=( u ,v ,2-u-v ) ,u 2+v 2 ≤1 . σ( u ,v )=( u ,v ,u 2+v 2 ) ,u 2+v 2≤
9 . Calcule a área da parte da superfície z = x^(3 // 2) + y^(3 // 2) , 0 = x = (8)/(9) e 0 = y = (9)/(16) x^2
11 . Calcule a área da superfície z = x 2 + y 2 compreendida entre os planos x + y = 1,x + y = 2,x = 0ey = 0
3. Seja f:K→R de classeC 1 no compacto K com fronteira de conteúdonulo e interior não vazio. Mostre que a área da superfície z = f( x ,y ) (istoé, da superfície σ dada por x=u ,y=vez=f( u ,v )) é dada
5 . Calcule a área da parte da superfície esférica x 2+y 2+z 2=1 que seencontra dentro do cone z ≥ x 2 + y ² ²