Calcule as seguintes integrais de superfície:
, onde S é o triangulo de vértices , e .
Passo 1
Galerinha, primeiro devemos entender a superfície que estamos integrando.
A equação que vamos usar é:
Passo 2
Sabemos que S é um triângulo de vértices , e
Vizualisando, nós temos que:
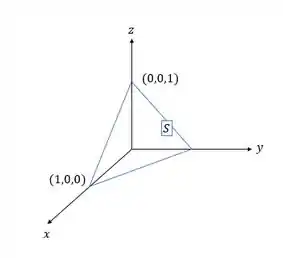
Da superfície desenhada acima, temos que a equação do plano geral é
Note que, e , logo temos que:
Vamos montar agora nosso plano :
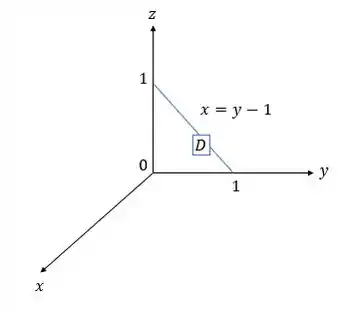
A região é dada por:
com
e
.
(Note que .)
Passo 3
Portanto, podemos então montar a integral que desejamos:
Isso implica que:
Passo 4
Resolvendo primeiro a integral de dentro, temos que:
Substituindo o intervalo de integração:
Simplificando os termos:
Agora resolvendo a integral de fora:
Substituindo o intervalo de integração: