Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.4 - Ex. 3

Deseja-se construir uma pela de zinco que tem a forma de superfície de equação z = 1 - x 2 , compreendida entre os planos y = 0 ,   z = 0 e o cilindro z = 1 - y 2 , y ≥ 0 . Se o metro quadrado do zinco custa A reais, calcule o preço total da peça.

Passo 1

Vamos inicialmente encontrar qual é a intersecção dos nossos cilindros:

z = 1 - x 2 z = 1 - y 2

Assim, igualando as equações, temos

1 - x 2 = 1 - y 2 x 2 = y 2 x = y

Ou seja, no plano x y , a intersecção representa a reunião das retas

y = x       e       y = - x

Além disso, como o cilindro está entre os planos y = 0 e z = 0 , então devemos ter

1 - x 2 ≥ 0 x 2 ≤ 1 - 1 ≤ x ≤ 1

Passo 2

Para calcular a área desejada, vamos precisar parametrizar nossa curva. Uma parametrização bastante natural será tomar

φ x , y = x ,   y ,   1 - x 2

A nossa área será dada pela seguinte integral:

S = ∬ D ∂ φ ∂ x × ∂ φ ∂ y   d x   d y

onde D é a região do plano x y mostrada na figura abaixo.

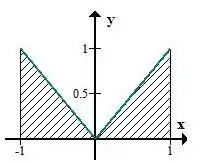
Passo 3

Assim, vamos começar calculando as derivadas:

∂ φ ∂ x = ∂ ∂ x x , ∂ ∂ x y , ∂ ∂ x 1 - x 2 ∂ φ ∂ x = 1,0 , - 2 x  

Também,

∂ φ ∂ y = ∂ ∂ y x , ∂ ∂ y y , ∂ ∂ y 1 - x 2 ∂ φ ∂ y = 0 ,   1 ,   0

Logo,

∂ φ ∂ x × ∂ φ ∂ y = i j k 1 0 - 2 x 0 1 0 ∂ φ ∂ x × ∂ φ ∂ y = 2 x ,   0 ,   1

Finalmente, temos:

∂ φ ∂ x × ∂ φ ∂ y = 2 x 2 + 0 2 + 1 2 = 4 x 2 + 1

Passo 4

Já estamos terminando.... “só” falta calcular a integral!

S = ∬ D 4 x 2 + 1   d x   d y

Veja que quando - 1 ≤ x ≤ 0 , temos 0 ≤ y ≤ - x e quando 0 ≤ x ≤ 1 , temos 0 ≤ y ≤ x . Assim,

S = ∫ - 1 0 ∫ 0 - x 4 x 2 + 1   d y   d x + ∫ 0 1 ∫ 0 x 4 x 2 + 1   d y   d x

Vamos calcular cada uma dessas integrais separadamente.

  • Cálculo da primeira integral:

    • I 1 = ∫ - 1 0 ∫ 0 - x 4 x 2 + 1   d y   d x I 1 = ∫ - 1 0 - x 4 x 2 + 1   d x

    Fazendo 4 x 2 + 1 = u , então 8 x   d x = d u ∴ x   d x = d u 8 . Quando x = - 1 , então u = 5 ; quando x = 0 , então u = 1 . Logo,

    I 1 = - ∫ 5 1 u 1 2 d u 8 = 1 8 ∫ 1 5 u 1 2   d u I 1 = 1 8 u 3 / 2 3 / 2 1 5 = 1 12 5 5 - 1

  • Cálculo da segunda integral:

I 2 = ∫ 0 1 ∫ 0 x 4 x 2 + 1   d y d x I 2 = ∫ 0 1 x   4 x 2 + 1   d x

Fazendo u = 4 x 2 + 1 , vemos que caímos exatamente na mesma integral anterior! Assim, segue que

I 2 = 1 12 5 5 - 1

Portanto,

S = ∬ D 4 x 2 + 1   d x   d y = I 1 + I 2 S = 1 6 5 5 - 1

Porém, como 1   m 2 custa A reais, então S m 2 custarão S A reais. Assim,

c u s t o = A 6 5 5 - 1   r e a i s

Resposta

O custo será de A 6 5 5 - 1 reais.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∫ ∫ S 2 zd S Onde S é a parte do paraboloide z=x ²+ y ² -2 ² ² abaixo do plano xy
Calcular ∫ ∫ S x y zd S Onde S é a superfície plana 3 x + 2 y+z=12 , delimitada pelos planos y = 0 , y = 2 , x = 0 , x = 1
Calcular ∫ ∫ S x 2 + y 2d S Onde S é a superfície lateral do cone x 2 4 + y 2 4 - z 2 9 = 0 , 0 ≤ z ≤ 16
Calcular ∫ ∫ S x zd S Onde S é a superfície y=x ² ², delimitada pelos planos z = 0 , z = 4 , x = 0,x = 2
Calcular ∫ ∫ S xz 2 + y 2d S Onde S é o hemisfério da frente x ²+y ²+z ²=9 ² ² ²