Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 6i

Calcule int int_B f (x , y) d x d y sendo dados:

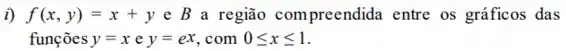
Passo 1

Chamando a integral dupla do teorema de Fubini de F :

F = int int_B f (x , y) d x d y

Podemos reescrevê-la como:

F = int int_B (x + y) d x d y

Ou:

F = int_a^b [int_(c (y))^(d (y)) (x + y) d x] d y = int_c^d [int_(a (x))^(b (x)) (x + y) d y] d x

A partir do esboço do conjunto B :

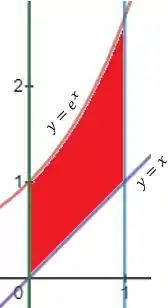
E dos intervalos dados pelo enunciado:

0 <= x <= 1

E

x <= y <= e^x

É possível resolver o cálculo.

Passo 2

Assim, é possível calcular:

F = int_0^1 [int_(y = x)^(y = e^x) (x + y) d y] d x

F = int_0^1 [x y + (y^2)/(2)] | [[y,=,e^x],[y,=,x]] d x

Substituindo o intervalo de integração em y :

F = int_0^1 [x e^x + (e^(2 x))/(2) - x^2 - (x^2)/(2)] d x

F = int_0^1 [x e^x + (e^(2 x))/(2) - (3)/(2) x^2] d x

Passo 3

Agora, integrando em relação a x , o primeiro termo deve ser resolvido através da integração por partes com u = x e d v = e^x d x , tal que d u = d x e v = e^x :

int x e^x d x = x e^x - int e^x d x = x e^x - e^x

Logo:

F = [x e^x - e^x + (e^(2 x))/(4) - (x^3)/(2)] | [[x,=,1],[x,=,0]]

E, substituindo o intervalo de integração:

F = [e^1 - e^1 + (e^2)/(4) - (1)/(2) + 1 - (1)/(4)]

F = (e^2)/(4) + (1)/(4) = (1)/(4) (1 + e^2)

Resposta

(1)/(4) (1 + e^2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla. ∬ Rx 1 + x yd A, R = 0 ,1 × 0 ,1
Calcule a integral dupla. ∬ R1 + x 2 1 + y 2 d A R = x ,y0 ≤ x ≤ 1,0 ≤ y ≤ 1 }
Calcule a integral dupla. ∬ Rx y 2 x 2 + 1 d A R = x ,y0 ≤ x ≤ 1,- 3 ≤ y ≤ 3 }
Calcule a integral dupla.∬_R^() cos ( x + 2 y ) d A , R = {(x , y)| 0 = x = pi , 0 = y = pi // 2 }
Calcule a integral dupla. ∬ Rxs e n ( x + y )d A,�� R = 0 , π 6 × 0 , π 3 ��