Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.4 - Ex. 2o
Calcule o volume do conjunto dado. (Sugerimos ao leitor desenhar o conjunto.)
e
Passo 1
O calculo de volume é dado por uma integral tripla. Mas será que não conseguimos facilitar nossa integral a fim de resumir ela pra uma integral dupla e sofrer menos?
Vamos primeiro desenhar nosso problema e ver qual é a cara dele. Pra isso, vamos usar o Geogebra, um software matemático e gratuito.
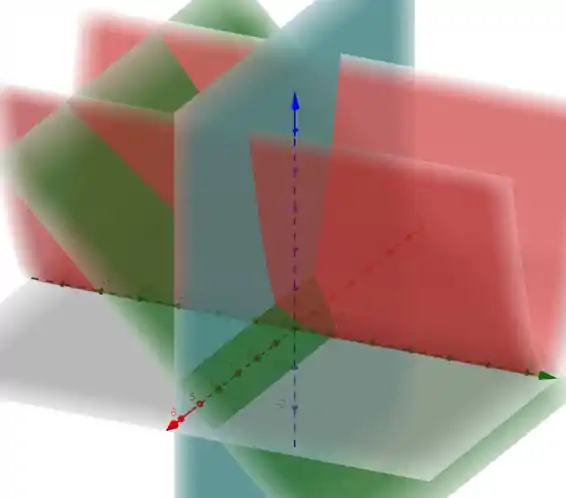
Parece feio, é, mas o nosso gráfico é a junção dessas três superfície.
É verdade que às vezes é importante entender como é a nossa superfície, mas se as funções são dadas, precisamos perceber qual é a lógica por trás da integração. Que não é esse caso hahaha .
Passo 2
Fazemos assim, suponha que nunca desenhamos o nosso gráfico. E sabemos que por definição, o volume de qualquer superfície é dado por
Até aqui, só a definição. seria o nosso conjunto de pontos que definem nosso volume.
Entretanto perceba que já está definido, assim temos que nosso volume pode ser escrito como
Sabemos que a integral de é então
Onde é a projeção do nosso volume no plano . Importante nós sabermos, que sempre será isso. Eliminamos uma coordenada, o conjunto restante é a projeção do volume, naquelas coordenadas restantes.
Assim tome a vista da nossa imagem, por cima
Podemos ver que o que nos sobra é uma parábola que relaciona e
Pela capacidade da observação hahah temos que
Enquanto varia de à .
Então temos que
Passo 3
Agora é resolver. A primeira integral fica
Eu sei, é chato, fazer essas distribuições, mas confia, não tem outra forma
Aahhhhhhh
E finalmente podemos escrever
E agora é só integrar
E agora, finalmente, queria agradecer a todos que me apoiaram até aqui e dizer do fundo do meu coração que
O livro apresenta como resposta , mas esse que vos ajudou acredita que o guidorizzi ta doidão hahaha