Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.4 - Ex. 2r
Calcule o volume do conjunto dado. (Sugerimos ao leitor desenhar o conjunto.)
e
Passo 1
O calculo de volume é dado por uma integral tripla. Mas será que não conseguimos fácilitar nossa integral a fim de resumir ela pra uma integral dupla e sofrer menos ?
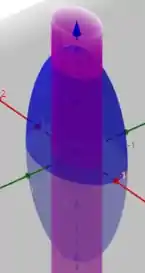
Se lembramos bem de Geometria Analitica, sabemos que a primeira superfície é um elipsóide (Azul) e outro um cilindro eliptico (Roxo)
Passo 2
Fazemos assim, suponha que nunca desenhamos o nosso gráfico. E sabemos que por definição, o volume de qualquer superfície é dado por
Até aqui, só a definição. seria o nosso conjunto de pontos que definem nosso volume.
Entretanto perceba que já está “definido”, mas vamos melhorar um pouco
Isolando
Feio, mas seguindo, dizemo que o volume pode ser escrito como
Sabemos que a integral de é então
Onde é a projeção do nosso volume no plano . Importante nos sabermos, que sempre será isso. Eliminamos uma coordenada, o conjunto restante é a projeção do volume, naquelas coordenadas restantes.
Perceba que nossa projeção é dada pelo nosso cilindro, o pois é ele que determina nossa superfície. Assim
Passo 3
Agora vamos fazer umas pequenas alterações em nosso sistema de coordenada para facilitar nossa resolução. Assim tome e , implicando que
Assim temos que
e
Lembrando que depois de toda parametrização, precisamos calcular nosso Jacobiano. Como todo estudante cansado de Calculo hahaha lembramos que o jacobiano em coordenada polares, quando temos e é . Desta forma
Que não é uma integral estranha de resolver. Faça uma substituição , na qual e . Assim temos
E assim finalmente temos que
No Livro não temos esse fator , entretanto em em nenhum momento tivemos alguma coisa dizendo que estamos limitados no plano . Então consideramos todo o volume.