Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.4 - Ex. 2n

Calcule o volume do conjunto dado. (Sugerimos ao leitor desenhar o conjunto.)

n) x 2 + y 2 + z 2 ≤ a 2 e z ≥ a / 2     a > 0

Passo 1

Nesse problema iremos calcular o volume do conjunto através da integral tripla. Para isso, vamos reduzir o problema de uma integral tripla para dupla, encontrando o novo conjunto K e os intervalos de integração. Vamos lá!

Pelo conjunto dado, o que estamos querendo calcular é a parte de cima da esfera dada pela imagem a baixo

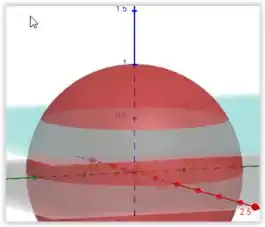
Passo 2

Primeiro vamos tentar definir nossos limites de integração e depois o conjunto K .

Olhando para nossa imagem do passo 1, temos que z se limite da seguinte forma

a 2 ≤ z ≤ a 2 - x 2 - y 2

E K será a projeção que essa superfície faz no plano x y ou seja, uma circunferência de raio a .

Passo 3

Temos que o volume é dado pela integral

∫ ∫ ∫ B d x ⋅ d y ⋅ d z = ∫ ∫ K ∫ a b d z ⋅ d x ⋅ d y

Substituindo nossos intervalos, chegamos que

∫ ∫ K ∫ a / 2 a 2 - x 2 - y 2 d z ⋅ d x ⋅ d y

= ∫ ∫ K [ a 2 - x 2 - y 2 - a / 2 ] d x ⋅ d y

Como definimos antes, temos que a nossa projeção é a circunferência x 2 + y 2 ≤ ρ 2 podemos usar uma parametrização em coordenadas polares e ficar com

x = ρ ⋅ cos ⁡ θ

y = ρ ⋅ sin ⁡ θ

Repara que quando z = a 2 , temos:

x 2 + y 2 + a 2 2 ≤ a 2

x 2 + y 2 ≤ 3 a 2 4

Então:

ρ = a 3 2

Daí:

0 ≤ ρ ≤ a 3 2

0 ≤ θ ≤ 2 π

Com o jacobiano sendo d x ⋅ d y = ρ ⋅ d ρ ⋅ d θ . Substituindo na integral e resolvendo, chegamos que

∫ 0 2 π ∫ 0 a 3 2 a 2 - ρ 2 - a / 2 ρ   d ρ   d θ

Separando em duas integrais para ficar mais fácil, vamos resolve-las separadamente.

A segunda é bastante tranquila e se resume da seguinte forma

∫ 0 2 π ∫ 0 a 3 2 a 2 ρ   d ρ   d θ = ∫ 0 2 π a 2 ρ 2 2 0 a 3 2 d θ = 3 π a 3 8

Já a segunda integral faremos uma substituição de a 2 - ρ 2 = u → ρ   d ρ = - d u / 2

E para os limites de integração:

a 2 - 0 = u 1 → u 1 = a 2

E

a 2 - a 3 2 2 = u 2 → u 2 = a 2 4

Assim temos

- ∫ 0 2 π ∫ a 2 a 2 4 u d u 2   d θ = - π 2 3 u 3 2 a 2 a 2 4 = - 2 π 3 a 3 8 + 2 π 3 a 3 = 7 π a 3 12

Desta forma nos sobra que

∫ ∫ ∫ B d x ⋅ d y ⋅ d z = 7 π a 3 12 - 3 a 3 π 8 = 14 a 3 π - 9 a 3 π 24 = 5 a 3 π 24

Resposta

∫ ∫ ∫ B d x ⋅ d y ⋅ d z = 5 a 3 π 24

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral tripla ∭ E x d V Onde E é limitado pelo parabolóide x = 4 y 2 + 4 z 2 e pelo plano x = 4
Calcule a integral tripla. ∭ E zd V , onde E é limitado pelo cilindro y 2 + z 2 = 9 e pelos planos x = 0 , y = 3 x e z = 0 no primeiro octante
Calcule a integral tripla. ∭ T x 2d V , onde T é o tetraedro sólido com vértices ( 0,0 , 0 ) , ( 1,0 , 0 ) , ( 0,1 , 0 ) e ( 0,0 , 1 )
Calcule a integral tripla. ∭ T x y zd V , onde T é o tetraedro sólido com vértices ( 0,0 , 0 ) , ( 1,0 , 0 ) , ( 1 , 1,0 ) e ( 1 , 0,1 )
Determine a região E para a qual a integral ∭ E 1 - x 2 - 2 y 2 - 3 z 2d V é máxima.