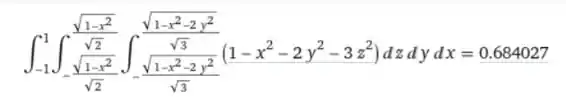Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 55
- Determine a região para a qual a integral tripla
é máxima.
- Use um sistema de computação algébrica para calcular o valor máximo exato da integral tripla na parte (a)
é máxima.
Passo 1
Fala, turma! Tudo sussa?
A questão tem duas partes. A parte (a) pede para acharmos a região onde essa integral
É máxima. Uma integral tem valor máximo na região onde a função que está sendo integrada é positiva. Assim, a gente evita regiões negativas que vão diminuir o valor da nossa integral. Então a nossa região que maximiza nossa integral será obtida pela análise de
A parte pede para usarmos um sistema de computação algébrica para acharmos o valor exato da integral que acharmos na parte a). Aqui podemos usar o WolframAlpha.
Vem entender!
Passo 2
Como já vimos, a integral tem o valor máximo, quando pegamos a maior região onde a função a ser integrada é positiva. Ou seja, precisamos que
Agora vamos manipular nossa inequação. Isolando o número e multiplicando a inequação por ), temos:
Agora é olharmos para essa inequação e tentarmos entender qual sólido ela representa.
Esse tipo de inequação se refere a um elipsoide sólido:
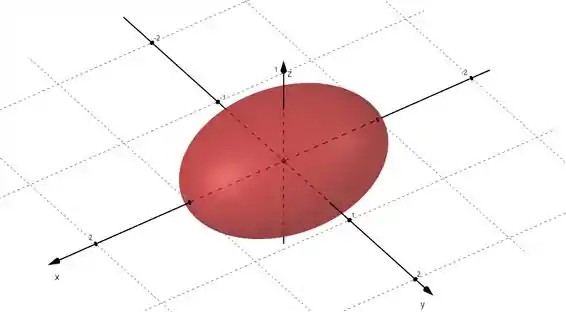
Que é a região onde a integral tem o seu valor máximo. Podemos descrever essa região da seguinte forma
Passo 3
- Antes de colocarmos nossa integral
em algum software de computação, precisamos dos limites de integração. Sabemos que os valores máximos da integral são aqueles na superfície:
Então vamos achar esses limites de integração em coordenadas retangulares:
- :
- :
- :
Fazendo na nossa equação, temos somente os valores no eixo :
Tirando a raiz quadrada da equação:
Então:
Para achar os limites de , fazemos , assim olhamos só para o plano :
Isolando :
Então nossos limites serão:
Para podemos só isolá-lo na nossa equação:
Então:
Aplicando a raiz quadrada na equação:
Então seu intervalo será:
Então nossa integral será:
Passo 4
Usando o software WolframAlpha para encontrar o valor da nossa integral, obtemos:
