Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 1g
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que
Passo 1
Temos para esse caso uma relação de y e x:
Essa relação parece meio nebulosa, mas se você reparar bem, dá pra ver que o lado direito da inequação se parece com a equação:
Que sabemos ser:
Ok! Mas se eu subtrair 1 do lado direito, eu tenho que somar um pra inequação se manter a mesma, então ficamos com:
Passando o termopara o lado esquerdo, temos:
Então o conjunto de todos os (x, y) que obedecem a essa relação vão dar um desenho mais ou menos assim:
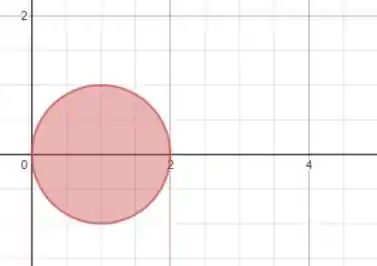
Gráfico que descreve todos os pontos (x, y) que obedece a
Ou seja, um gráfico de uma circunferência de centro (1,0).
Como sabemos, pela regra da reta vertical, não podemos trabalhar com equações onde para um dado y temos dois valores de x, ou seja, precisamos achar uma função y(x):
Ok, agora que temos a equação que descreve a metade superior da circunferência podemos usar o método aprendido para descobrir o volume dessas área rotacionada no eixo y.
Como!?
Bem, sabemos que se pegarmos vários retângulos com largura infinitesimal (ou seja, dx) e a altura variando do meio da circunferência (que no nosso caso é o eixo x) até a metade superior da circunferência (ou seja, a altura vai ser a função temos a área do retângulo dado, se rotacionarmos esse retângulo em relação ao eixo y, tendo o raio dessa rotação( que será a distância do eixo y e o centro do retângulo, que é x) conseguimos calcular o volume de cada cilindro:
Fazendo o somatório desses cilindros teremos o volume dessa rotação, que, como já vimos na teoria, pode ser calculado pela integral:
Lembrando que só estamos considerando a área dos retângulos que estão acima do eixo x, mas como a equação é simétrica ao eixo x podemos multiplicar por 2 e teremos o resultado da rotação de toda circunferência e não só a da parte superior:
Dá pra ver no gráfico que os limites de integração vão ser a distância entre os raios da circunferência sobre o eixo x, que é quando y=0, ou seja:
Caímos numa inequação do tipo:
Ok! Agora temos a integral usada pro cálculo e seus limites de integração. Ficamos com:
Vamos achar o resultado dessa integral:
Passo 2
Vemos que essa equação é muito difícil de ser feita por substituição, mas se fosse uma equação:
Seria fácil de substituir por ,então faremos com que exista um x-1. Para subtrair 1 temos que somar 1, ficará assim:
Separamos o que queremos substituir do 1 que sobrou:
Fazendo a distributiva, temos:
Separamos em duas integrais pela propriedade da soma:
Para , usamos o que foi discutido acima, fazemos a substituição e então fica:
E a segunda substituição feita:
Pela propriedade que diz:
Se os limites de integração (superior e inferior) forem iguais, essa integração vale.
Com isso ficamos só com.
Para , usaremos também
Esse é um caso clássico de substituição trigonométrica. Funciona assim:
se parece muito com Pitágoras, não é?
Não viu? vou mostrar, então:
Coloque um triângulo de lados a,b e c.
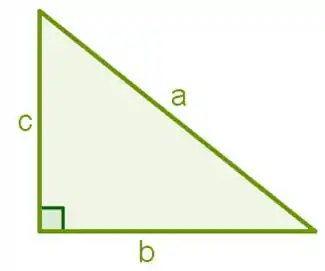
Concorda comigo que o valor de um dos catetos vai valer ? E também que se colocarmos teta alí entre a hipotenusa e a base, teremos essas relações:
e
Para o nosso caso teremos:
Lados a=1, c=u e e, com isso, ficaremos com:
Sabemos da relação que diz: , por isso ficaremos com:
Pra finalizar, se temos e podemos coloca-los de volta na equação:
Ou seja:
Agora somando: