No cálculo de uma integral dupla sobre uma região D , obtivemos uma soma de integrais iterada como a que segue: ∬ D f x , y d A = ∫ 0 1 ∫ 0 2 y f x , y d x d y + ∫ 1 3 ∫ 0 3 - y f x , y d x d y Esboce a região D e expresse a integral dupla como uma integral iterada com ordem de integração contrária.

∬ D f x , y d A = ∫ 0 2 ∫ x / 2 1 f x , y d y d x + ∫ 0 2 ∫ 1 3 - x f x , y d y d x

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 64

No cálculo de uma integral dupla sobre uma região , obtivemos uma soma de integrais iterada como a que segue:

Esboce a região e expresse a integral dupla como uma integral iterada com ordem de integração contrária.

Passo 1

Hi, pessoal. Tudo bem?

A questão quer o esboço da região D através do cálculo de uma soma de integrais dada pra gente, e depois pede pra expressar essa mesma integral mas com a ordem de integração contrária. Moleza, né?

Vamos analisar a região D de cada uma das integrais, ou seja, os limites de integração:

Passo 2

Abaixo, temos o esboço das regiões:

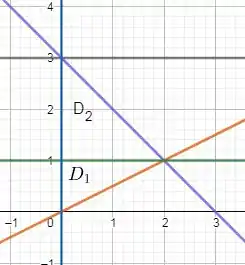
Passo 3

Invertendo a ordem da integral, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 9-18, escreva a integral iterada de ∬ R d A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.

Como as integrais duplas são avaliadas como integrais iteradas? A ordem da integração importa? Como os limites de integração são determinados? Dê exemplos.

Como as substituições em integrais duplas são descritas comotransformações de regiões bidimensionais? Dê um exemplocom cálculo.

Carga elétrica total sobre uma placa circular A distribui-ção de carga elétrica sobre uma placa circular de raio R metrosé s(r, u) = kr(1 – sen u) coulomb/m2 (sendo k uma constante).Integre s sobre a