Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 49
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, saiu melhor. Se seu programa também produz curvas de nível, trace o diagrama de contornos da mesma função e compare.
49-
Passo 1
Olá, meu querido amigo. Vamos juntos resolvermos essa atividade. Aqui iremos precisar de um software gráfico.
Aqui iremos utilizar o GeoGebra 3D para plotarmos o gráfico tridimensional da figura. Para plotarmos a curva de nível, podemos utilizar o GeoGebra 2D fazermos a seguinte igualdade:
Assim teremos diversas curvas de nível.
Passo 2
Colocando a equação no GeoGebra 3D:
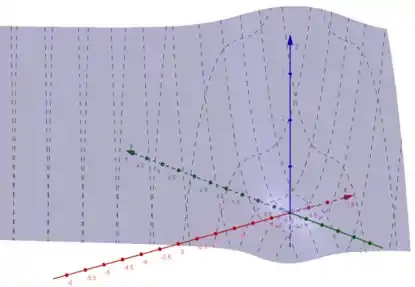
Agora para curva de nível, escolhemos valores arbitrários para :
E assim temos o nosso gráfico:
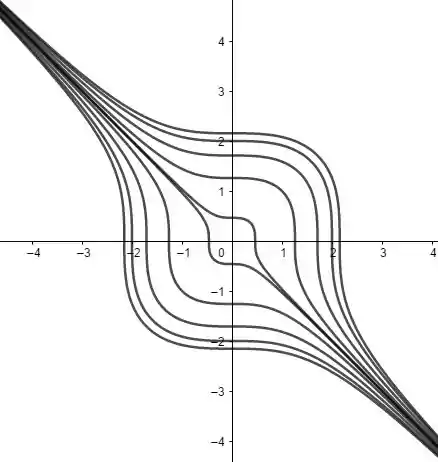
É uma cebola hahah
Passo 3
A tendência é que o nível zero tenda a ficar na reta e o nível negativo (que está no plano inferior de ) tenda a contornar a origem em direção ao primeiro quadrante e parte do gráfico no plano positivo tenda a contornar a origem no terceiro quadrante. Bem é isso que os dois gráficos nos dizem.
O melhor gráfico é aquele que permite visualizar melhor o comportamento da função, com a visualização que colocamos, conseguimos visualizar bem o comportamento do nosso gráfico, mas isso pode ser subjetivo, pois depende também do que você busca visualizar no momento em que analisa o gráfico da função.
Resposta
Gráficos do passo 1 e 2.