Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 43
Faça o mapa de contornos da função mostrando várias curvas de nível.
Passo 1
Fala ai galerinha. De boa? Vamos entender um pouco sobre a questão, o que ela pede e como podemos resolver? Bora lá!
O objetivo é esboçar o mapa de contornos da função , mostrando várias curvas de nível. Isso ajuda a visualizar como a função se comporta no plano, identificando regiões de valores constantes.
Vamos
- Definir as curvas de nível de , onde é uma constante.
- Selecionar valores de , sendo eles positivos, negativou ou o zero.
- Desenhar as curvas e considerando o valor de .
Agora é só resolver!
Passo 2
As curvas terão níveis iguais a e que podem ser encontradas igualando com da seguinte forma:
E dessa forma teremos a seguinte equação:
Ou:
A equação representada uma parábola deitada, ou uma parábola horizontal. E a equação serão parábolas deitadas com vértice em ou seja, quando for zero (que será o zero da função) será .
Passo 3
Para cada valor de
Para :
A equação define uma parábola abrindo para cima.
Para :
A equação define uma parábola abrindo para baixo.
Para
A curva de nível é a parábola
Passo 4
O mapa de contornos da função mostrará várias curvas de nível que nos ajudam a entender o comportamento da função no plano. Cada curva representa um conjunto de pontos onde a diferença entre e é constante, formando parábolas com diferentes aberturas dependendo do valor de .
Isso nos dá as seguintes curvas de nível.
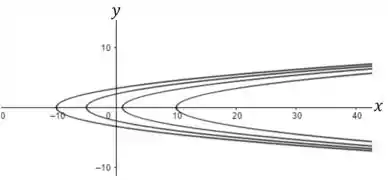
Quando mais a esquerda a parábola irá ficar e quando mais a direita.
Resposta
Gráfico do passo 2.