Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 1l

1 - Desenhe as curvas de nível e esboce o gráfico.

L - z = f x ,   y dada por x 2 + 4 y 2 + z 2 = 1 , z ≥ 0

Passo 1

L e t r a   L :

Bem, sabemos que uma curva de nível k pode ser encontrada fazendo z = f x ,   y = k . Nesse caso...

x 2 + 4 y 2 + z 2 = 1   →

x 2 + 4 y 2 + k 2 = 1   →

x 2 + 4 y 2 = 1 - k 2

CARA! O que é isso aí? SIMMMM!

Como k é sempre constante, x 2 + 4 y 2 = 1 - k 2 são elípses! Onde o máximo valor de k é 1 e o mínimo 0 , já que a imagem da função f x ,   y é 0 ,     1 .

Passo 2

Claro, como k é constante, para cada valor de k , teremos elipses de tamanhos diferentes!

Vamos desenhar algumas delas aqui então:

Para k = 0 (em vermelho) e k = 3 4 :

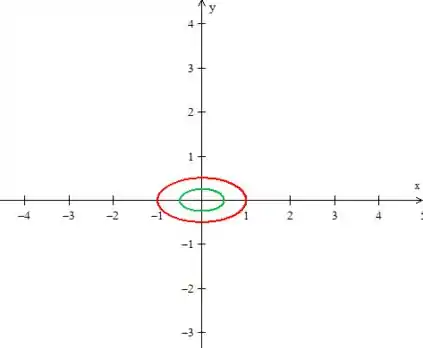
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

66. Descreva como o gráfico de g é obtido a partir do gráfico de f a) g x , y = f ( x - 2 ,y ) b) g x , y = f ( x ,y + 2 ) c) g x , y = f ( x + 3 ,y - 4 )