1 - Desenhe as curvas de nível e esboce o gráfico.
G -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
Tenha em mente que é sempre constante! De modo que...
Como ...
Então deve ser . Repare que essa equação representa retas constantes e paralelas ao eixo ! Mas atenção! .
Vamos desenhar algumas dessas retas aqui então:
Para , e :
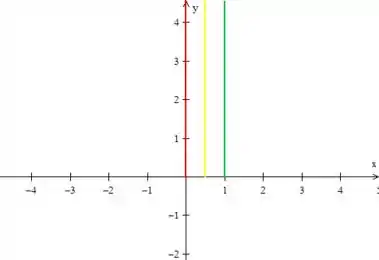
Resposta