Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.6 - Ex. 12

Certa pessoa que se encontra em A , para atingir C , utilizará na travessia do rio (de 100   m de largura) um barco com velocidade máxima de 10   k m / h ; de B a C utilizará uma bicicleta com velocidade máxima de 15   k m / h . Determine B para que o tempo gasto no percurso seja o menor possível.

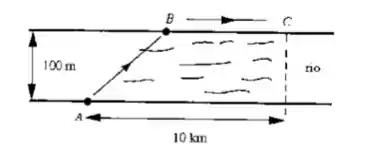
Passo 1

Vamos primeira definir a equação para o tempo total gasto:

t = s b a r c o v b a r c o + s b i c i c l e t a v b i c i c l e t a = A B - 10 + B C - 1 5

Onde A B - é a distância entre A e B e B C - é a distância entre B e C . Vamos supor um triângulo A B D :

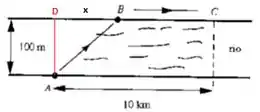
Passo 2

Portanto,

cos ⁡ B Â D = A D - A B - = 0,1 A B - → A B - = 0,1 cos ⁡ B Â D

tan ⁡ B Â D = x A D - = x 0,1 → x = 0,1 ∙ tan ⁡ B Â D

Como D C - = B C - + x :

D C - = B C - + x → 10 = B C - + 0,1 ∙ tan ⁡ B Â D

B C - = 10 - 0,1 ∙ tan ⁡ B Â D

Passo 3

Substituindo na equação do tempo total:

t = A B - 10 + B C - 15 = 0,1 10 cos ⁡ B Â D + 10 - 0,1 ∙ tan ⁡ B Â D 15

t = 1 15 0,15 cos ⁡ B Â D + 10 - 0,1 tan ⁡ B Â D

A função t admitirá um mínimo quando d t d B Â D = 0 .

Passo 4

Vamos derivar a função agora:

d t d B Â D = 1 15 0,15 cos ⁡ B Â D + 10 - 0,1 tan ⁡ B Â D ' = 0

1 15 0,15 sec ⁡ B Â D tan ⁡ B Â D + 0 - 0,1 sec 2 ⁡ B Â D = 0

0,15 sec ⁡ B Â D tan ⁡ B Â D - 0,1 sec 2 ⁡ B Â D = 0

sec ⁡ B Â D 0,15 tan ⁡ B Â D - 0,1 sec ⁡ B Â D = 0

Assim,

sec ⁡ B Â D = 0 ou 0,15 tan ⁡ B Â D - 0,1 sec ⁡ B Â D = 0

Como sec ⁡ B Â D = 1 cos ⁡ B Â D ≠ 0 ,

0,15 tan ⁡ B Â D - 0,1 sec ⁡ B Â D = 0

0,15 tan ⁡ B Â D = 0,1 sec ⁡ B Â D

0,15 ∙ sin ⁡ B Â D cos ⁡ B Â D = 0 , 1 cos ⁡ B Â D

0,15 sin ⁡ B Â D = 0 , 1

sin ⁡ B Â D = 0 , 1 0,15 = 2 3

Passo 5

Lembrando da relação fundamental da trigonometria:

sin 2 ⁡ B Â D + cos 2 ⁡ B Â D = 1

2 3 2 + cos 2 ⁡ B Â D = 1

cos 2 ⁡ B Â D = 1 - 4 9 = 5 9

cos ⁡ B Â D = 5 3

Assim,

x = 0,1 ∙ tan ⁡ B Â D = 0,1 ∙ sin ⁡ B Â D cos ⁡ B Â D = 0,1 ∙ 2 3 5 3 = 0,1 ∙ 2 5 = 0,2 5 ∙ 5 5 = 0,2 5 5

x = 0,04 5   k m = 40 5   m

Prontinho!!!

Resposta

40 5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . (Use os gráficos e as transformações das Seções 1.2 e 1.3.) f x = | x |
Encontre os números críticos da função. F x = x 4 5 x - 4 2
Encontre os números críticos da função. f x = 2 x 3 + x 2 + 2 x
Encontre os valores máximo e mínimo absolutos de f no intervalo dado. f x = x 3 - 6 x 2 + 5 ,[ - 3,5 ]
Encontre os números críticos da função. h t = 3 t - a r c s e nt