Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.8 - Ex. 16b
Considere a curva de intersseção das superfícies definidas de equações e . Determine:
Os pontos do hiperboloide onde o plano tangente é perpendicular ao vetor encontrado no item .
Passo 1
Bom galera, a questão quer que a gente encontre os pontos em que o plano tangente é perpendicular ao vetor do item anterior.
Pra isso a gente precisa lembrar que por definição o vetor grádiente é esse vetor perpendicular a o ponto de uma superfície, logo perpendicular também a um plano tangente. Assim:
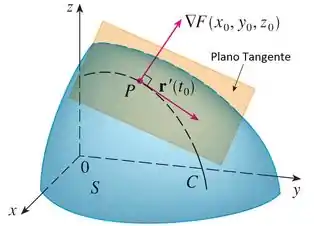
Passo 2
Belezinha, então a gente precisa que o nosso vetor gradiente nos pontos sejam iguais ao nosso vetor direção. Então vamos começar pegando as derivadas parciais pra encontrar o vetor gradiente:
Passo 3
Show de bolinhas, agora a gente precisa encontrar os pontos em que esse vetor gradiente seja igual aquele do item passado , lembrando que como é um vetor direção pode ser tanto negativo como positivo, logo podemos montar uma equação assim:
Então podemos motar umas equaçõezinhas e calcular os valores dos pontos:
Onde encontramos , agora :
Ficamos com:
E agora :
Ficamos com:
Logo temos os pontos:
e
E prontinho. 😊