Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.3 - Ex. 5

Considere o escoamento bidimensional v → x , y =   - y x 2 + y 2 i → + x x 2 + y 2 j → .

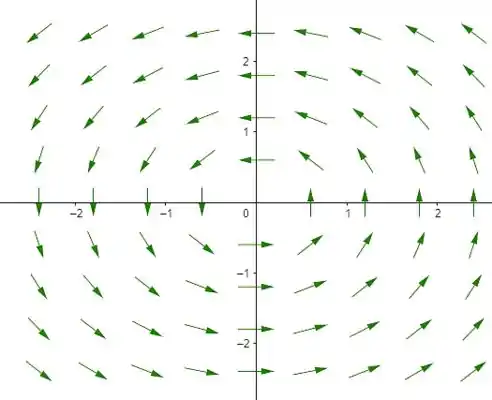
  1. Desenhe tal campo.
  2. Calcule r o t   v → e interprete-o.

Passo 1

  1. Vamos fazer desenho do campo primeiro. O vetor v → ( x , y ) é tangente à circunferência que passa pela pela origem, no ponto ( x , y ) . Com isso a trajetórias das partículas do campo são circunferências de centro na origem também.

    2. Passo 2

  2. Vamos calcular o rotacional agora. Como temos só duas dimensões, podemos fazer:

r o t = ∂ Q ∂ x - ∂ P ∂ y k →

Sendo que aqui nós temos:

Q = x x 2 + y 2   e   P =   - y x 2 + y 2

Bora lá então...

r o t   v → = 1 x 2 + y 2 - 2 x x x 2 + y 2 2 - - 1 x 2 + y 2 - - y 2 y x 2 + y 2 2 k →

= x 2 + y 2 - 2 x 2 x 2 + y 2 2 - - x 2 - y 2 + 2 y 2 x 2 + y 2 2 k →

= - x 2 + y 2 + x 2 - y 2 x 2 + y 2 2

= 0 x 2 + y 2 2

r o t   v → =   0 →

Como o rotacional deu zero, concluímos que o campo é irrotacional.

Resposta

  1. Desenho.
  2. r o t   v → = 0 → . Irrotacional.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se F → = r → / r p , ache d i v F → . Existe algum valor de p para o qual d i vF → = 0 ?
Vimos que todos os campos vetoriais na forma F → = ∇ g satisfazem a equação r o tF → = 0 e que todos os campos vetoriais na forma F → = r o t G → satisfazem a equação d i vF → = 0 (supondo a continuid
Demonstre a identidade, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se f for um campo escalar e F → e G → forem campos vetoriais, então f F → , F → ⋅ G → e F → × G → serão
Demonstre a identidade, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se f for um campo escalar e F → e G → forem campos vetoriais, então f F → , F → ⋅ G → e F → × G → serão
Use a primeira identidade de Green (exercício 33 ) para demonstrar a segunda identidade de Green: ∬ ( f ∇ 2 g - g ∇ 2 f )d A = ∮ ( f ∇ g - g ∇ f ) ⋅ n →d s