Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.2 - Ex. 8-b
8. Considere a função g(x, y) = onde f (u) é uma função de uma variável real a valores reais, contínua em [a, b], 0 ≤ a
b. Utilizando coordenadas polares mostre que o volume de B é
Passo 1
Temos alguns métodos para calcular o volume de um solido. O meotodo do Cilindro por exemplo diz que
Que tem a tem a seguinte ideia
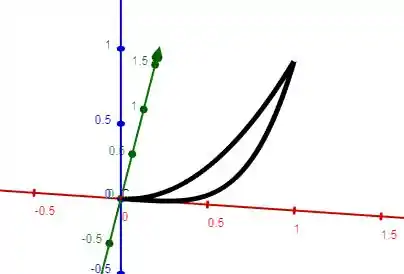
Pegamos duas curvas, integramos a diferença entre elas, e assim achamos a área interna. E rotacionamos formando assim um solido. Se a nossa curva de baixo for o eixo x. Por exemplo se
Teremos algo como a imagem abaixo
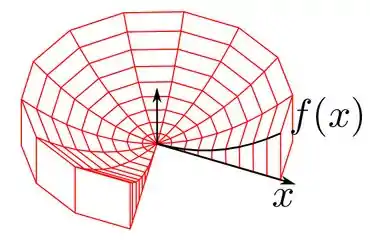
Passo 2
NO nosso caso temos que
Logo nossa fórmula genérica
Se reduz a
Visto que nossa função
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)