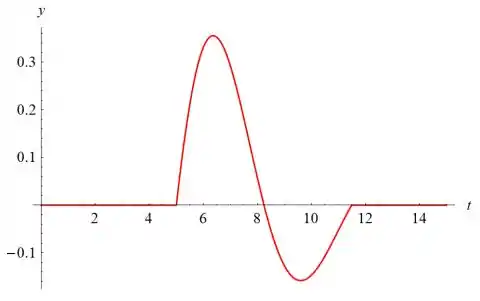
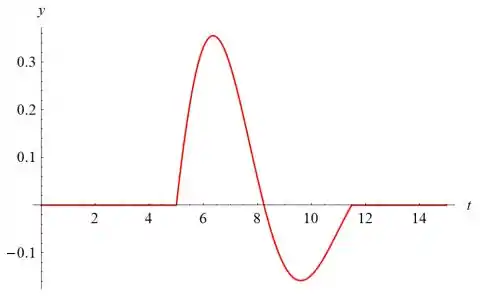
Considere, novamente, o sistema no Exemplo 1 desta seção, no qual uma oscilação é gerada por um impulso unitário em t = 5. Suponha que desejamos colocar o sistema em repouso após exatamente um ciclo — ou seja, quando a resposta volta, pela primeira vez, à posição de equilíbrio movendo-se no sentido positivo.
- Determine o impulso que deve ser aplicado ao sistema para alcançar esse objetivo. Note que k é o tamanho do impulso e é o instante de sua aplicação.
- Resolva o problema de valor inicial resultante e faça o gráfico de sua solução para confirmar que se comporta da maneira especificada.
Passo 1
O sistema no Exemplo 1 é governado pelo problema do valor inicial,
Resolver esse problema com a transformação de Laplace gera
Abaixo está um gráfico de y (t) versus t
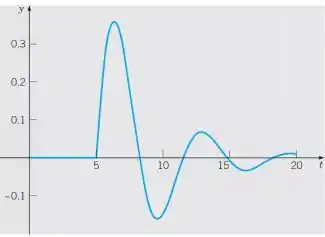
O novo impulso precisa ser aplicado após a conclusão de uma oscilação. Use esse fato para determinar
k será encontrado mais tarde. No momento, resolva o problema do valor inicial com o segundo impulso aplicado.
Passo 2
Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:
Consequentemente, as derivadas se transformam da seguinte maneira.
Aplique a conversão Laplace nos dois lados da EDO:
Passo 3
Aplique as condições iniciais e
Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):
Passo 4
Agora, basta resolver esta equação e achar sua inversa, chegando em:
Passo 5
Uma vez que t assume o valor de , a amplitude do primeiro termo é
e a amplitude do segundo termo é
Para o segundo termo cancelar o primeiro, exigimos que
Com esse valor de k e o valor encontrado para , o gráfico de y (t) versus t exibe o resultado desejado.