Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.4 - Ex. 16

Determinado sistema mola-massa satisfaz o problema de valor inicial

u ' ' + 1 4 u ' + u = k g ( t ) ,   u ( 0 ) = 0 ,   u ' ( 0 ) = 0 ,

em que g ( t ) = u 3 / 2 ( t ) - u 5 / 2 ( t ) e k > 0 é um parâmetro.

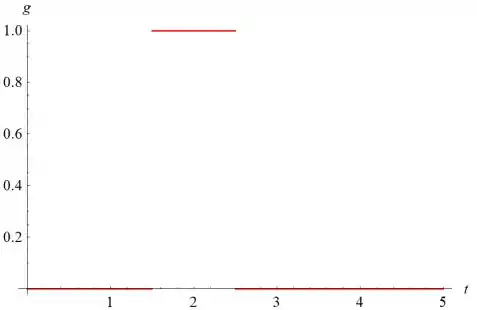
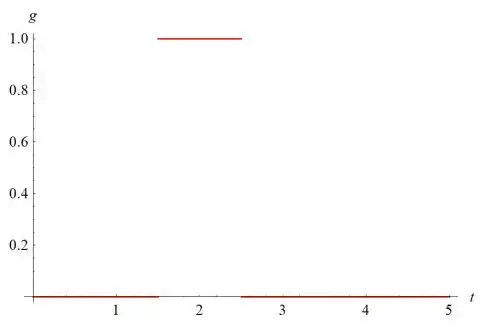
  1. Esboce o gráfico de g(t). Note que é um pulso de tamanho unitário que se estende por uma

    2. unidade de tempo.

  2. Resolva o problema de valor inicial.
  3. Desenhe o gráfico da solução para k = 1/2, k = 1 e k = 2. Descreva as características

    4. principais da solução e como elas dependem de k.

  4. Encontre, com duas casas decimais, o menor valor de k para o qual a solução u(t) alcança o

    5. valor 2.

  5. Suponha que k = 2. Encontre o instante τ após o qual |u(t)| t > τ .

Passo 1

Letra a:

Passo 2

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função u(t) é definida aqui como:

U ( s )   =   L { u ( t ) } = ∫ 0 ∞ e - s t u ( t )   d t

Consequentemente, a primeira e a segunda derivadas se transformam da seguinte maneira.

L { d u d t } = s U ( s )   -   u ( 0 )

L { d ² u d t ² } = s ² U ( s )   -   s u ( 0 ) - u ' ( 0 )

Aplique a conversão Laplace nos dois lados da EDO:

L { u ' ' + 1 4 u ' + u } = L { k g ( t ) } = L { k [ u 3 / 2 ( t ) - u 5 / 2 ( t ) ] }

L { u ' ' } + L { 1 4 u ' } + L { u } = L { k g ( t ) } = L { k u 3 / 2 ( t ) } - L { k u 5 / 2 ( t ) }

[ s ² U ( s )   -   s u ( 0 ) - u ' ( 0 ) ] + 1 4 [ s U ( s )   -   u ( 0 ) ] + [ U ( s ) ] = k ∫ 0 ∞ e - s t [ u 3 / 2 ( t ) ] d t - k ∫ 0 ∞ e - s t [ u 5 / 2 ( t ) ] d t

Passo 3

Aplique as condições iniciais, u ( 0 ) = 0   e   u ' ( 0 ) = 0 .

[ s ² U ( s ) ] + 1 4 s U ( s ) + U ( s ) = k ∫ 3 / 2 ∞ e - s t d t - k ∫ 5 / 2 ∞ e - s t d t ;

Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para U, (a solução transformada):

( s ² + 1 4 s + 1 ) U ( s ) = k ( 1 s e - 3 s / 2 ) - k ( 1 s e - 5 s / 2 )

U ( s ) = k s ( s ² + 1 4 s + 1 ) e - 3 s / 2 - k s ( s ² + 1 4 s + 1 ) e - 5 s / 2

Passo 4

Usando frações parciais para achar a inversa:

k s ( s ² + 1 4 s + 1 ) = A s + B s + C s ² + 1 4 s + 1

s = 0 :   k = A

s = 1 :   k = 9 4 A + B + C

s = 2 :   k = 11 2 A + 4 B + 2 C

Resolvendo, chegamos em:

A = k ,   B = - k ,   e   C =   - k / 4

U ( s ) = ( k s + - k s - k 4 s ² + 1 4 s + 1 ) e - 3 s / 2 - ( k s + - k s   - k 4 s ² + 1 4 s + 1 ) e - 5 s / 2

Agora, basta resolver esta equação e achar sua inversa!

u ( t ) = L - 1 { U ( s ) } = L - 1 { ( k s + - k s - k 4 s ² + 1 4 s + 1 ) e - 3 s / 2 - ( k s + - k s   - k 4 s ² + 1 4 s + 1 ) e - 5 s / 2 }

Chegando em:

u ( t ) = { k - k e - ( t - 3 2 ) / 8 c o s [ 63 8 ( t - 3 2 ) ] - k 63 e - ( t - 3 2 ) / 8 s e n [ 63 8 ( t - 3 2 ) ] } H ( t - 3 2 )

- { k - k e - ( t - 5 2 ) / 8 c o s [ 63 8 ( t - 5 2 ) ] - k 63 e - ( t - 5 2 ) / 8 s e n [ 63 8 ( t - 5 2 ) ] } H ( t - 5 2 )

Passo 5

Letra c:

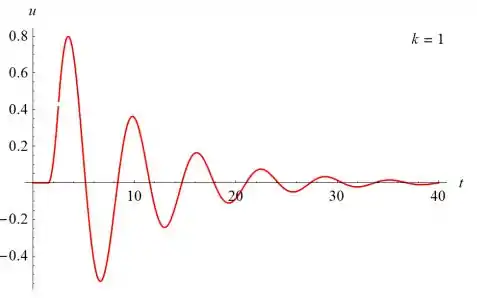
Abaixo estão vários gráficos de u(t) versus t para u(t) versus t para vários valores de k

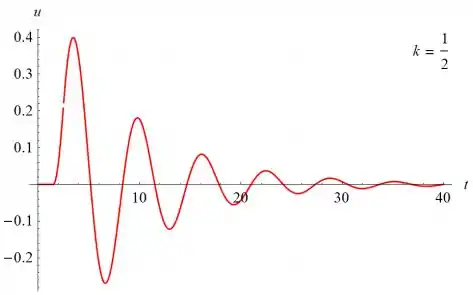
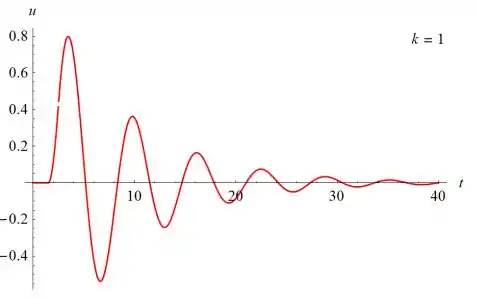
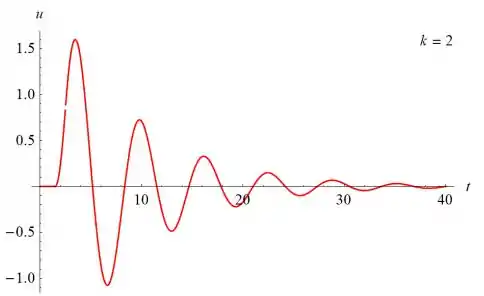
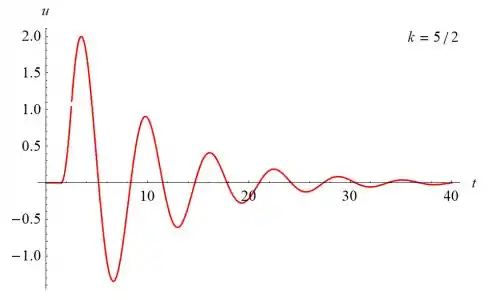
Passo 6

Letra d:

O primeiro máximo de u parece ser proporcional a k; o máximo é 2 quando k ≈ 2.51. A solução começa a oscilar em t = 3/2 e tem uma amplitude que decai com o tempo.

Passo 7

Letra e:

Ajuste os limites inferior e superior do gráfico k = 2 para -0,1 e 0,1, respectivamente, para encontrar o tempo em que a amplitude é menor que 0,1 para todos os tempos posteriores.

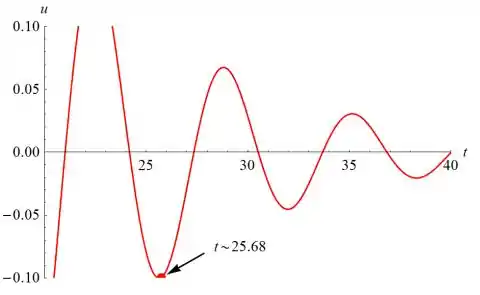
Resposta

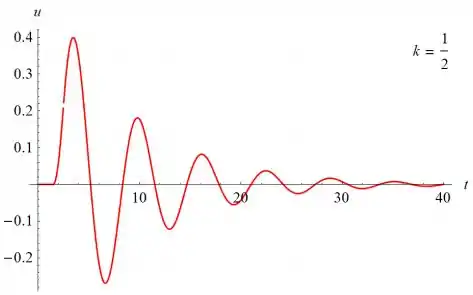
  2. u ( t ) = { k - k e - ( t - 3 2 ) / 8 c o s [ 63 8 ( t - 3 2 ) ] - k 63 e - ( t - 3 2 ) / 8 s e n [ 63 8 ( t - 3 2 ) ] } H ( t - 3 2 ) - { k - k e - ( t - 5 2 ) / 8 c o s [ 63 8 ( t - 5 2 ) ] - k 63 e - ( t - 5 2 ) / 8 s e n [ 63 8 ( t - 5 2 ) ] } H ( t - 5 2 )

  4. O primeiro máximo de u parece ser proporcional a k; o máximo é 2 quando k ≈ 2.51. A solução começa a oscilar em t = 3/2 e tem uma amplitude que decai com o tempo.
  5. t=25.68
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.12. y ' ' + 3 y ' + 2 y = 0 ; y 0 = 1 ; y ' 0 = 0
Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.14. y ' ' - 4 y ' + 4 y = 0 ; y 0 = 1 ; y ' 0 = 1
Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.15. y ' ' - 2 y ' + 4 y = 0 ; y 0 = 2 ,y ' 0 = 0
Use o resultado d d t e t = e t e ( 1 ) desta seção para calcular L e t
Nos problemas 3 e 4, suponha que uma função y ( t ) tenha a propriedade y 0 = 1 e y ' 0 = - 1 . Encontre a transformada de Laplace da expressão dada y ' ' + 3 y '