Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.4 - Ex. 15
Considere o problema de valor inicial
(a) Resolva o problema de valor inicial e faça o gráfico de sua solução para 0 ≤ t ≤ 5.
(b) Determine onde a solução tem valor zero.
(c) Determine as coordenadas (t0, y0) do ponto de mínimo.
(d) Mude a segunda condição inicial para y′(0) = b e encontre a solução como função de b.
Depois encontre o valor crítico de b que separa as soluções que permanecem positivas das que
acabam se tornando negativas.
Passo 1
Olá...
Essa questão não é espelho, mas vamos dar uma refletida nela... rsrs. Brincadeiras à parte, o que a gente vai ter que fazer primeiro é encontrar a solução homogênea e descobrir as constantes, e nós temos as condições que são , e .
Vamos transformar essa equação em uma equação do 2º grau. Então passa a ser , passa a ser , e é o termo independente.
Sendo: .
Então para encontrar o usamos a fórmula de Bhaskara.
Lembrando que:
- Se o resultado do , teremos duas raízes reais diferentes, e a equação característica vai ser:
- Se o resultado do , teremos duas raízes reais iguais, e a equação característica vai ser:
- Se o resultado do , teremos duas raízes complexas, e a equação característica vai ser:
Com isso em mãos vamos substituir na fórmula de Bhaskara:
Sendo raízes iguais, a solução geral será do tipo:
Passo 2
Vamos usar nossa arma secreta: através do valor inicial dado, vamos descobrir o valor das constantes. Seja:
Vamos ter:
E seja:
Vamos ter:
A solução geral vai ser então:
E o nosso gráfico:
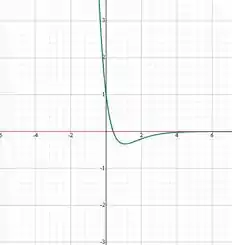
Passo 3
A letra (b) pede pra dizer onde a solução tem valor zero. Como somos seres evoluídos e inteligentes, vamos utilizar o nosso gráfico pra ter essas informações sem precisar fazer conta. . O gráfico cruza o eixo em , que é igual a , mas vamos deixar em fração que é como tá no livro.
Já a letra (c) pede pra determinar o gráfico no ponto mínimo. E pra otimizar nosso tempo de nosso vamos ver isso pelo gráfico. A solução tem ponto mínimo em .
Passo 4
E a nossa letra (d) pede pra mudar a segunda condição inicial para e encontrar a solução como função de . Depois encontre o valor crítico de b que separa as soluções que permanecem positivas das que acabam se tornando negativas. Mudando a condição:
Com o segundo termo sendo dominante a solução depende do sinal dele, então o valor crítico é .
Resposta
- O gráfico cruza o eixo em .
- A solução tem ponto mínimo em .
- , o valor crítico é .