Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 3
3.
(a) Resolvendo a Eq. (12) numericamente, mostre que a parte real das raízes complexas muda de sinal quando .
(b) Mostre que um polinômio de grau três da forma tem uma raiz real e duas raízes imaginárias puras só se .
(c) Aplicando o resultado do item (b) à Eq. (12), mostre que a parte real das raízes complexas muda de sinal quando 9.
Passo 1
Assim como fizemos no exercício anterior, como o problema nos permite usar uma ferramenta computacional, vamos utilizar aqui então o WOLFRAMALPHA para resolver a nossa equação 12:
A equação que nos dá os autovalores de todo o nosso sistema 3x3 até aqui estudado!
Para mostrar que de fato a parte real muda de valor em, utilizemos dois valore de : e , um acima e outro abaixo, saca? Com esses valores vamos substituir na equação de e depois jogar no WOLFRAMALPHA e dar enter pra vermos qual é a resposta gerada!
Vamos nessa?
Primeiro substituindo ...
As duas soluções complexas foram:
Substituindo agora ...
Dessa vez, os valores imaginários foram:
Provando de fato que o sinal da parte real muda em .
Passo 2
Para provar isso, veja que podemos trocar por na equação:
Com , podemos provar que é solução da nossa equação:
Fatorando então usando o método de Briot Ruffini:
Onde é a solução da equação. Aplicando o método, ou seja, abaixando 1 depois multiplicando por ele e somando o próximo e assim por diante...
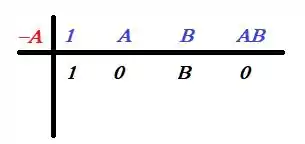
Isso significa que outra equação que vai surgir para resolver a equação é:
O que significa que poderemos fatorar a equação...
Assim:
A solução dessa equação quadrática:
De fato é um número imaginário puro considerando .
Agora, perceba que essa fatoração em:
Só foi possível por considerar . Caso, seja qualquer outro valor, não seria solução provocando um valor diferente de no termo de nessa expressão:
Então necessariamente surgirá um fator misto na fatoração:
Essa na solução por báskara surge com um número real aqui em negrito:
O que impedirá a existência de um imaginário puro, saca?
Passo 3
Vejamos, a nossa equação cúbica é:
Dividindo todo mundo por :
Então, podemos falar agora que...
Como vimos, a forma de termos um imaginário puro é se...
Então...
Multiplicando todo mundo por ...
Então de fato para qualquer outro valor de , não teremos imaginário puro. O que prova que pra cima de , vai existir parte real e ela vai ser positiva, como já vimos na letra A. E pra baixo de , ela vai ser negativa.
Resposta
Ei, a resposta está no passo a passo :)