Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.6 - Ex. 1a

Considere a aplicação definida por

x = u v e y = v - u

Determine a imagem D no plano x y do retângulo R no plano u v de vértices 0,1 , 1,1 , 1,2 e 0,2 .

Passo 1

Bom galera, a gente tem que transformar a região R do plano u v em uma região D do plano x y , e pra isso temos as equações:

x = u v

y = v - u

Passo 2

Belezinha, vamos então encontrar os pontos na região D :

0,1 → x = 0 ⋅ 1 = 0 ; y = 1 - 0 = 1 → 0,1

1 , 1 → x = 1 ⋅ 1 = 1 ; y = 1 - 1 = 0 → 1 , 0

1 , 2 → x = 1 ⋅ 2 = 2 ; y = 2 - 1 = 1 → 2 , 1

0 , 2 → x = 0 ⋅ 2 = 0 ; y = 2 - 0 = 2 → 0 , 2

Passo 3

Show de bolinhas, agora podemos delimitar nossa região graficamente, fica bem assim:

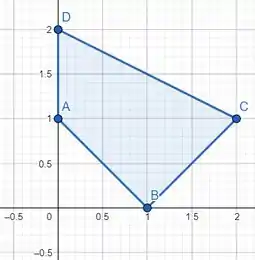
E prontinho. 😊

Resposta

0,1

1,0

2,1

0,2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Determine a imagem do conjunto S sob a transformação dada. S é o quadrado limitado pelas retas u = 0 , u = 1 , v = 0 , v = 1 ; x = v , y = u 1 + v 2
Utilize a transformação dada para calcular a integral. ∬ R x 2 d A , onde R é a região limitada pela elipse 9 x 2 + 4 y 2 = 36 ; x = 2 u , y = 3 v
Determine a imagem do conjunto S sob a transformação dada. S é a região triangular com vértices 0,0 , 1,1 , 0,1 ; x = u 2 , y = v
Utilize a transformação dada para calcular a integral. ∬ R x y d A , onde R é a região do primeiro quadrante limitada pelas retas y = x e y = 3 x e pelas hipérboles x y = 1 , x y = 3 ; x = u v , y = v