Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.7 - Ex. 6
Aplique o Teorema de Steiner ao item do Exercício 4.
Passo 1
Vamos olhar para o início da nossa seção 5.7 e nos atentar para a seguinte relação
Que é definido como nosso momento de inércia, na qual e é nossa densidade volumétrica. Assim agora precisamos só aplicarmos nossa equação. Claro que estou aqui para ajuda-los ...
O teorema de Steiner pode ser lido no enunciado do Exercício 5. ((Teorema de Steiner ou dos iexos paralelos). Seja o momento de inércia em relação a um eixo que passa pelo centro de massa de um corpo e o momento de inércia em relação a um eixo paralelo, a uma distância .) Assim temos que
Passo 2
Aplicando o Teorema de Steiner, temos então que
Do item (a) temos que
Então apenas substituindo e somando o nosso termos, temos
Simples não ? Deixamos a baixo o item (b) no nosso exercício 4 para que você possa comparar e distinguir a complexidade de aplicar ou não o nosso Teorema de Steiner.
Passo 3
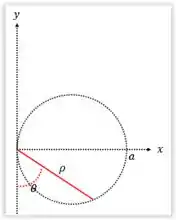
b) Aqui queremos calcular o momento de icércia com relação ao eixo . Desta forma vamos apelar a nosso amigo pitagora e tomar que qualquer ponto dista do eixo por .
Usando nossas coordenadas cilíndricas, temos
Assim temos que
Assim temos que
Com isso ficamos com
Em nossa integral da e agora vamos resolver para
Então temos
Como cosseno é uma função par e estamos integrando em um intervalo simétrico, ficamos com
E agora como integra o cosseno a quarta?
Vamos fazer que . Assim usando integral por partes , temos
A primeira parte da integral claramente é nula, visto que e . Assim nos sobra que
E lembrando nossas relações trigonométricas, ou deduzindo a partir de , temos que
Assim ficamos com
Outra relação importante que devemos lembrar dedizindo a partir de é
Assim novamos nossa integral se resume em
Desta forma temos por fim
E depois de muito sofrer neste nosso item, temos
Resposta
Ei, a resposta está no passo a passo :)