Considere a aplicação definida pelas equações
e
Utilizando , calcule , onde é a imagem no plano da região no plano limitada pelas retas , .
Passo 1
Bom galera, a gente precisa calcular a área da região . Vamos começar mudando as variáveis na integral dupla, que é bem assim:
Onde temos:
Passo 2
Belezinha, a gente precisa calcular o determinante jacobiano, usando as derivadas parciais:
Então, colocamos os valores:
Passo 3
Show de bolinhas, então nossa integral fica:
Agora vamos delimitar a região :
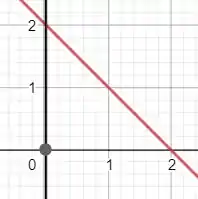
A região fica:
Passo 4
Por fim, montamos as integrais e calculamos:
Antes vamos substituimos e :
Integramos a primeira vez:
E integramos denovo:
E prontinho. 😊