Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 1
Considere a transformação dada por e . Desenhe o conjunto onde é o retângulo e .
Passo 1
Quando o está fixo em , fazemos o variar de , daí obtemos uma circunferência de raio , enquanto quando o está fixo em , a transformação faz o retângulo virar um círculo de raio .
Ou seja, nesse caso em que temos o , a gente fica com o conjunto desenhado aqui:
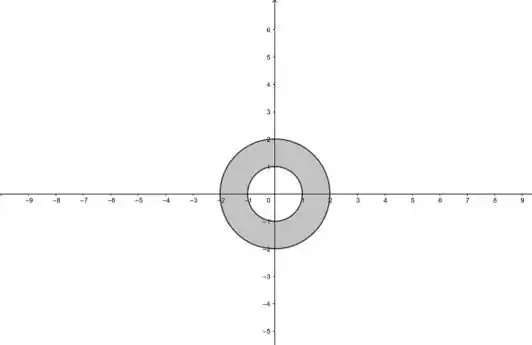
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 2 ∫ 0 4 - x 2e - x 2 - y 2 d y d x
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 1 / 2 ∫ 3 y 1 - y 2x y 2 d x d y
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .3-
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .4-
29- Calcule a integral iterada, convertendo-a antes para coordenadas polares: ∫ 0 1 ∫ 0 1 - x 2 e x 2 + y 2 d y d x