Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 19
Construa uma função que seja contínua em e que seja derivável em todos os pontos, exceto nos números inteiros.
Passo 1
Dos exercícios anteriores vimos que uma função derivável é aquela em que a função é suave, ou seja, aquela em que não apresenta um bico em seu esboço.
Uma função que é diferenciável em todo conjunto dos reais é a função , olha só:
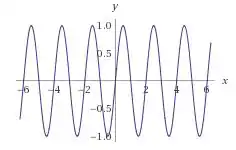
Ela é bem comportada, toda diferenciável. Suave em todos os pontos: ou seja, não apresenta bicos.
Passo 2
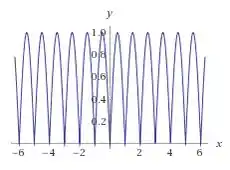
Mas e como deixar esse gráfico com um bico? Ah! É aqui que entra a função modular! Lembra que a função módulo deixa tudo que é negativo positivo? Então! Em um gráfico isso não é diferente! Se agora fizermos , toda parte negativa passa a ser positiva e justamente nas raízes da função, ou seja
Ela vai apresentar um bico, saca só:
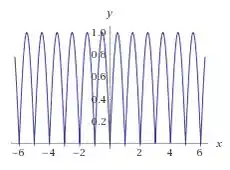
Esses bicos representam os pontos onde a função não é diferenciável.
Ok?
Vamos pra próxima!
Resposta
