Coordenadas polares. Suponha que substituamos as coordenadas polares x = r cos ⁡ θ e y = r sen ⁡ θ em uma função derivável w = f x ,y .a. Mostre que ∂ w ∂ r = f x cos ⁡ θ + f y sen ⁡ θ e 1 r ∂ w ∂ θ = - f x sen ⁡ θ + f y cos ⁡ θ b. Resolva as equações no item (a) para expressar f x e f y em termos de ∂ w / ∂ r e ∂ w / ∂ θ .c. Mostre que f x 2 + f y 2 = ∂ w ∂ r 2 + 1 r 2 ∂ w ∂ θ 2

Enunciado

Oi pessoal, no item a. queremos mostrar as derivadas e . Então primeiro iremos fazer o diagrama de árvore referente a :

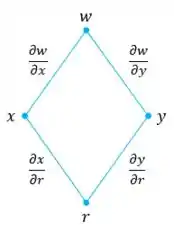
Com isso, através da Regra da Cadeia, temos:

Considerando que . E sabemos que , então:

E , logo:

Sendo assim:

O diagrama de árvore de :

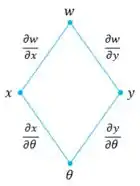
Com isso, através da Regra da Cadeia, temos:

Para fazermos as derivadas, vamos relembrar que:

Sendo assim:

Substituindo na equação:

No item b. iremos resolver as equações do item a. para expressar e em termos de e . Então, temos as equações:

Na equação (I), vamos isolar da equação:

Substituindo na equação (II):

Para , temos:

Voltando na equação (I):

Sendo assim, para :

E por fim, no item c. iremos mostrar que:

Logo:

Sabemos que:

Sendo assim:

Ufa, finalmente acabamos, esse foi um exercício mais teórico, mas espero ter conseguido te ajudar! Até mais pessoal.

Respostas nos Passos.