Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 24

Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada.

∂ w ∂ s para w = g x ,   y , x = h r ,   s ,   t , y = k r ,   s ,   t

Passo 1

Oi galerinha, tudo bem com vocês? Antes de iniciarmos este exercício, vamos relembrar a Regra da Cadeia de uma variável independente e duas variáveis intermediárias.

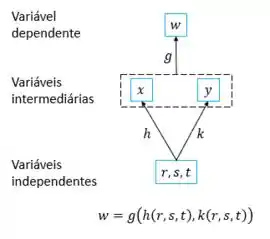
Se w = f x ,   y é diferenciável e se x = x t , y = y t forem funções deriváveis de t , então a composta w = f x t ,   y t será uma função derivável de t :

d w d t = ∂ f ∂ x d x d t + ∂ f ∂ y d y d t

O diagrama de árvore na margem propõe uma maneira conveniente de se lembrar da regra da cadeia. A “verdadeira” variável independente na função composta é t , enquanto x e y são variáveis intermediárias (controladas por t ) e z é a variável dependente.

De acordo com o enunciado, temos os seguintes dados:

Passo 2

Apesar de serem três variáveis independentes, queremos apenas para ∂ w / ∂ s

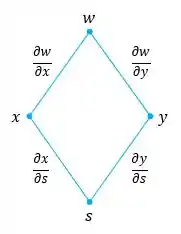
Então a fórmula para a Regra da Cadeia:

∂ w ∂ s = ∂ w ∂ x ∂ x ∂ s + ∂ w ∂ y ∂ y ∂ s

Resposta

∂ w ∂ s = ∂ w ∂ x ∂ x ∂ s + ∂ w ∂ y ∂ y ∂ s

Exercícios de Livros Relacionados

Use a regra da cadeia para achar d z // d t .z = x^2 + y^2 + x y , x = s e n t e y = e^t
Use a regra da cadeia para achar d z // d t .z = sqrt(1 + x^2 + y^2) , x = ln t e y = cos t
1-6. Use a Regra da Cadeia para achar d z d t ou d w d t .3. z = s e nx ⋅ cos ⁡ y ,x = t ,y = 1 t
1-6. Use a Regra da Cadeia para achar d z d t ou d w d t .1. z = x y 3 - x 2 y ,x = t 2 + 1 ,y = t 2 - 1
1-6. Use a Regra da Cadeia para achar d z d t ou d w d t .4. z = 1 + x y ,x = tan ⁡ t ,y = a r c tan ⁡ t