Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 48

Curva no espaço. Seja w = x 2 e 2 y cos ⁡ 3 z . Encontre o valor de d w / d t no ponto 1 , ln ⁡ 2 ,   0 na curva x = cos ⁡ t , y = ln ⁡ t + 2 , z = t .

Passo 1

Oi pessoal, tudo bem com vocês? Vamos lá! Primeiramente a gente vai desenhar o diagrama de árvore:

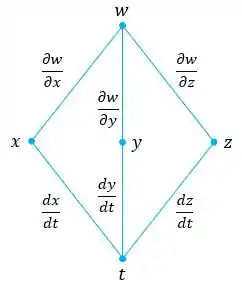
Com o diagrama, conseguimos definir a Regra da Cadeia:

d w d t = ∂ w ∂ x d x d t + ∂ w ∂ y d y d t + ∂ w ∂ z d z d t

Passo 2

Então vamos calcular as derivadas da função w = x 2 e 2 y cos ⁡ 3 z , já substituindo o ponto 1 , ln ⁡ 2 ,   0 :

∂ w ∂ x = 2 x e 2 y cos ⁡ 3 z

= 2 ∙ 1 ∙ e 2 ln ⁡ 2 cos ⁡ 3 ∙ 0

= 2 ∙ 2 2 ∙ 1

∂ w ∂ x = 8

∂ w ∂ y = 2 x 2 e 2 y cos ⁡ 3 z

= 2 ∙ 1 2 ∙ e 2 ln ⁡ 2 cos ⁡ 3 ∙ 0

= 2 ∙ 2 2 ∙ 1

∂ w ∂ y = 8

∂ w ∂ z = - 3 x 2 e 2 y sen ⁡ 3 z

= - 3 ∙ 1 2 ∙ e 2 ln ⁡ 2 sen ⁡ 3 ∙ 0

= - 3 ∙ 2 2 ∙ 0

∂ w ∂ z = 0

Passo 3

Agora iremos calcular as derivadas parciais de x = cos ⁡ t :

d x d t = - sen ⁡ t

Para y = ln ⁡ t + 2 :

d y d t = 1 t + 2

E para z = t :

d z d t = 1

Passo 4

Voltando na equação da Regra da Cadeia, substituindo os valores encontrados:

d w d t = 8 ∙ - sen ⁡ t + 8 ∙ 1 t + 2 + 0 ∙ 1

d w d t = - 8 sen ⁡ t + 8 t + 2

Pelo enunciado, sabemos que t = z = 0 , logo:

d w d t = - 8 sen ⁡ 0 + 8 0 + 2 = 0 + 4

d w d t = 4

Ufa, finalmente conseguimos acabar este exercício! Espero ter conseguido te ajudar, até mais!

Resposta

d w d t = 4

Exercícios de Livros Relacionados

Encontrando uma função com derivadas parciais de segunda ordem condicionadas Suponha que f seja uma função duas vezes diferenciável de r , que r = x 2 + y 2 + z 2 e que f x x + f y y + f z z = 0 . Mos
Nos Exercícios 1-6, (a) expresse d w / d t como uma função de t, utilizando a regra da cadeia, expressando w em termos de t e diferenciando diretamente com relação a t. Em seguida, (b) calcule dw/dt n
Nos Exercícios 1-6, (a) expresse d w / d t como uma função de t, utilizando a regra da cadeia, expressando w em termos de t e diferenciando diretamente com relação a t. Em seguida, (b) calcule dw/dt n
Nos Exercícios 1-6, (a) expresse d w / d t como uma função de t, utilizando a regra da cadeia, expressando w em termos de t e diferenciando diretamente com relação a t. Em seguida, (b) calcule dw/dt n
Nos Exercícios 1-6, (a) expresse d w / d t como uma função de t, utilizando a regra da cadeia, expressando w em termos de t e diferenciando diretamente com relação a t. Em seguida, (b) calcule dw/dt n