Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 35
As curvas de nível (isotérmicas) são mostradas para a temperatura da água (em °C) em Long Lake (Minnesota) em como uma função de profundidade e da época do ano. Estime a temperatura do lago em de junho (dia ) em uma profundidade de e em de junho (dia ) em uma profundidade de .
Passo 1
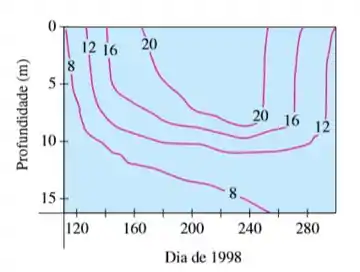
Eaee, belezinha?? Bom... o enunciado nos deu o seguinte gráfico que descreve as curvas de nível (isotérmicas) para a temperatura da água:
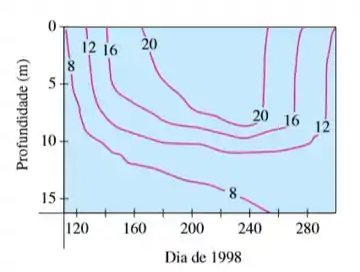
Note que essas curvas estão em função da profundidade e do dia.
Queremos estimar a temperatura do lago em de junho (dia ) em uma profundidade de e em de junho (dia ) em uma profundidade de .
Para isso, devemos selecionar esses pontos no respectivo dia e profundidade mostrados para verificarmos a curva mais próxima desses pontos.
Passo 2
A temperatura no dia , a uma profundidade de é dada no ponto dado em vermelho:
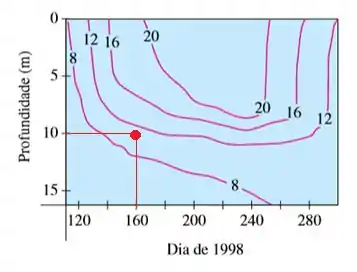
Esse ponto se encontra entre as curvas de e , mais próxima da de , então a temperatura estimada é de .
Passo 3
Já no dia , a uma profundidade de , é o ponto , também dado em vermelho:
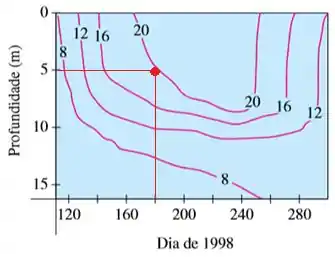
Veja que está entre as curvas de e , porém muito próxima a de ).
Então estimamos a temperatura para .
Resposta
e