Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 13

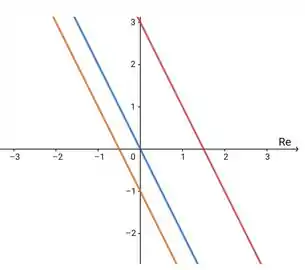
13. Suponha que T x , y = 2 x + y ° C represente uma distribuição de temperatura no plano x y .

a) Desenhe as isotermas correspondentes às temperaturas: 0°C, 3°C e -1°C.

b) Raciocinando geometricamente, determine os pontos de mais alta e mais baixa temperatura do círculo   x 2 + y 2 ≤ 4 .

Passo 1

Temperatura é   T x , y o enunciado pede para 0°C, então, é só substituir

  T x , y = 2 x + y

0 = 2 x + y

Isolando y,

y = - 2 x

Temos uma reta decrescente que passa pela origem e passa pelo ponto 1 , - 2 , assim

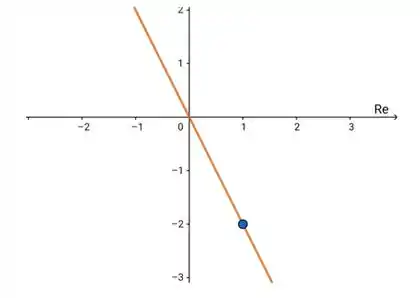
Passo 2

Temperatura é   T x , y o enunciado pede para 3°C, então, é só substituir

  T x , y = 2 x + y

3 = 2 x + y

Isolando y,

y = 3 - 2 x

Temos uma reta decrescente que cruza o eixo x em 3 2 , 0 e cruza o eixo y em 0,3 , assim

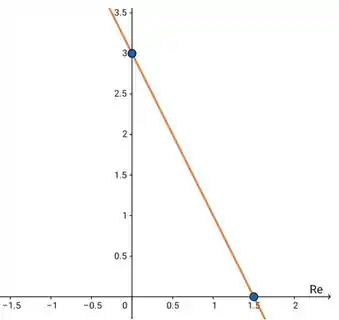
Passo 3

Temperatura é   T x , y o enunciado pede para -1°C, então, é só substituir

  T x , y = 2 x + y

- 1 = 2 x + y

Isolando y,

y = - 1 - 2 x

temos uma reta decrescente que cruza o eixo y em   0 , - 1   e cruza o eixo x em - 1 2 , 0 , assim

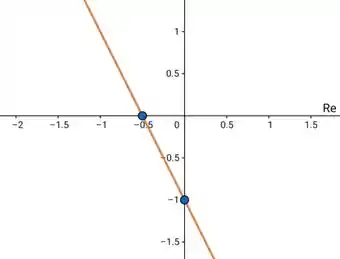
Passo 4

Os pontos de mais baixa e mais alta temperatura da circunferência   x 2 + y 2 ≤ 4

  y ≤ ± 4 - x 2  

substituindo em T x , y = 2 x + y

T 1 x , 4 - x 2 = 2 x + 4 - x 2

  T 2 x , - 4 - x 2 = 2 x - 4 - x 2

Ponto de mínimo e máximo de uma função, deriva e iguala a zero

2 x + 4 - x 2 ' = 0                                                                   2 x - 4 - x 2 ' = 0

                      2 - x 4 - x 2 = 0                                                                                       2 + x 4 - x 2 = 0

Isolando x,

                      2 - x 4 - x 2 = 0                                                                                       2 + x 4 - x 2 = 0

                      x 4 - x 2 = 2                                                                                 x 4 - x 2 = - 2

                                                x 4 - x 2 2 = 2 2                                                                             x 4 - x 2 2 = - 2 2

                      x 2 4 - x 2 = 4                                                                                 x 2 4 - x 2 = 4

x 2 2 - x 2 + x = 4 ,   s e   x ≠ ± 2

x 2 = 16 - 4 x 2

x 2 + 4 x 2 = 16

5 x 2 = 16

  x = ± 16 5 = ± 4 5 = ± 4 5 5

substituindo no y,

  y = ± 4 - x 2

  y = ± 4 - 16 5

  y = ± 20 - 16 5

  y = ± 4 5

  y = ± 2 5 = ± 2 5 5

então, o ponto de mais baixa temperatura e mais alta temperatura é de, respectivamente, - 4 5 5 , - 2 5 5 ,   4 5 5 , 2 5 5 .

Resposta

m a i s   b a i x a - 4 5 5 , - 2 5 5

m a i s   a l t a   4 5 5 , 2 5 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico da função.f (x , y) = y
Esboce o gráfico da função. f x , y = 1 - x 2
Faça o mapa de contornos da função mostrando várias curvas de nível. f x , y = x + y
Faça o mapa de contornos da função mostrando várias curvas de nível. f x , y = x - y 2
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, saiu melhor. Se seu programa também produz curvas de nível, trace o diagrama de cont